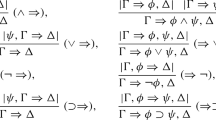Abstract
We present sound, (weakly) complete and cut-free tableau systems for the propositional normal modal logicsS4.3, S4.3.1 andS4.14. When the modality □ is given a temporal interpretation, these logics respectively model time as a linear dense sequence of points; as a linear discrete sequence of points; and as a branching tree where each branch is a linear discrete sequence of points.
Although cut-free, the last two systems do not possess the subformula property. But for any given finite set of formulaeX the “superformulae” involved are always bounded by a finite set of formulaeX* L depending only onX and the logicL. Thus each system gives a nondeterministic decision procedure for the logic in question. The completeness proofs yield deterministic decision procedures for each logic because each proof is constructive.
Each tableau system has a cut-free sequent analogue proving that Gentzen's cut-elimination theorem holds for these latter systems. The techniques are due to Hintikka and Rautenberg.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
R. A. Bull,An algebraic study of Diodorean modal systems Journal of Symbolic Logic 30(1), 1965, pp. 58–64.
R. A. Bull,Review of ‘Melvin Fitting, Proof Methods for Modal and Intuitionistic Logics, Synthese Library, Vol. 169, Reidel, 1983’ Journal of Symbolic Logic 50, 1985, pp. 855–856.
R. A. Bull andK. Segerberg,Basic modal logic, In D. Gabbay and F. Guenthner, editors,Handbook of Philosophical Logic, Volume II: Extensions of Classical Logic, pp. 1–88. D. Reidel 1984.
M. Fitting,Proof Methods for Modal and Intuitionistic Logics, volume 169of Synthese Library, D. Reidel, Dordrecht, Holland 1983.
M. Fitting,First order modal tableaux Journal of Automated Reasoning 4, 1988, pp. 191–213.
R. I. Goldblatt,Logics of Time and Computation, CSLI Lecture Notes Number 7, CSLI Stanford 1987.
G. E. Hughes andM. J. Cresswell,Introduction to Modal Logic Methuen, London 1968.
G. E. Hughes andM. J. Cresswell,A Companion to Modal Logic Methuen, London 1984.
E. J. Lemmon andD. Scott,An Introduction To Modal Logic American Philosophical Quarterly, Monograph Series, Basil Blackwell, Oxford 1977.
W. Rautenberg,Modal tableau calculi and interpolation Journal of Philosophical Logic 12, 1983, pp. 403–423.
W. Rautenberg,Corrections for modal tableau calculi and interpolation by W. Rautenberg, JPL 12 (1983) Journal of Philosophical Logic 14, 1985, p. 229.
W. Rautenberg, Personal communication, December 5th, 1990.
K. Segerberg,An essay in classical modal logic (3 vols.), Technical Report Filosofiska Studier, nr 13, Uppsala Universitet, Uppsala 1971.
T. Shimura,Cut-free systems for the modal logic S4.3 and S4.3GRZ Reports on Mathematical Logic 25, 1991, pp. 57–73.
S. Valentini,A syntactic proof of cut elimination for GL lin Zeitschrift für Mathematische Logik und Grundlagen der Mathematik 32, 1986, pp. 137–144.
J. F. A. K. van Benthem andW. Blok,Transitivity follows from Dummett's axiom Theoria 44 1978, pp. 117–118.
P. Wolper,Temporal logic can be more expressive Information and Control 56, 1983, pp. 72–99.
J. J. Zeman,Modal Logic: The Lewis-Modal Systems, Oxford University Press 1973.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Goré, R. Cut-free sequent and tableau systems for propositional Diodorean modal logics. Stud Logica 53, 433–457 (1994). https://doi.org/10.1007/BF01057938
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF01057938