Abstract
The present paper is concerned with a general approach to the construction and the numerical analysis of stable methods solving semi-infinite convex programs and variational inequalities of elliptical type in case where the considered problems are incorrect. The approach which is based on the application of the PROX-regularization (cf. Martinet, 1970; Ekeland and Temam, 1976; Rockafellar, 1976; Brézis and Lions, 1978; Lemaire, 1988) secures the strong convergence of the minimizing sequence. The possibility of the algorithmical realization is described and depends on the smoothness properties of the solutions.
Similar content being viewed by others
References
Alart, P. and Lemaire, B. (1991), Penalization in Non-Classical Convex Programming Via Variational Convergence,Math. Programming 51, 307–331.
Brézis, H. and Lions, P. L. (1978), Produits infinis de resolvantes,Israel J. Math. 29, 329–345.
Ekeland, I. and Temam, R. (1976),Convex Analysis and Variational Problems, North-Holland Publ. Co., Amsterdam.
Ficchera, G. (1972),Boundary Value Problems of Elasticity with Unilateral Constraints, Springer Verlag, Berlin-Heidelberg-New York.
Glowinski, R., Lions, J. L., and Tremoliers, R. (1981),Numerical Analysis of Variational Inequalities, North-Holland Publ. Co., Amsterdam.
Grossmann, Ch. and Kaplan, A. A. (1979),Strafmethoden und modifizierte Lagrangemethoden in der nichtlinearen Optimierung, Teubner Texte, Leipzig.
Hlavacek, L., Haslinger, J., Necas, L., and Lovicek, J. (1986),Solution of Variational Inequalities in Mechanics, MIR, Moscow.
Kaplan, A. A. (1988), On the Stability of Solution Methods for Convex Optimization Problems and Variational Inequalities,Trans. of the Inst. of Math., Siberian Branch of Acad. of Sci. USSR,10, 132–159.
Kaplan, A. A. (1990), On the Convergence of Methods of Solving Variational Inequalities with Weakly Coercive Operators,Soviet Math. Dokl. 41, 11–15.
Kaplan, A. A. and Tichatschke, R. (1989), Variational Inequalities and Semi-Infinite Convex Programming Problems, Preprint No. 27, Inst. of Math., Siberian Branch of Acad. of Sci. USSR.
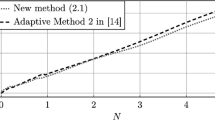
Kaplan, A. A. and Tichatschke, R. (1991), A Study of Iterative Processes for the Solution of Ill-Posed Convex Variational Problems.Soviet Math. Dokl. 42(3), 747–750.
Kustova, W. I. (1985), Solution Method for a Contact Problem with Weakly Coercive Operator,Optimization (Novosibirsk)36, 31–48.
Lemaire, B. (1988), Coupling Optimization Methods and Variational Convergence,Intern. Series of numerical mathematics 84, 163–179, Birkhäuser Verlag Basel.
Martinet, R. (1970), Regularisation d'inequations variationelles par approximations successive,RIRO 4, 154–159.
Mosco, U. (1969), Convergence of Convex Sets and of Solutions of Variational Inequalities,Advances in Mathematics 3, 510–585.
Pankov, A. D. (1979), Discrete Application of Convex Sets and the Solution of Variational Inequalities,Math. Nachrichten 91, 7–22.
Rockafellar, R. T. (1976), Monotone Operators and the Proximal Point Algorithm,SIAM J. Control and Optimization 14(5), 877–898.
Tichatschke, R. (1985), Semi-Infinite Programming Problems,Math. Control Theory, Banach Center Publ., Warszawa,14, 543–554.
Author information
Authors and Affiliations
Additional information
Supported by Deutsche Forschungsgemeinschaft under grant Ti 191/1-1.
Rights and permissions
About this article
Cite this article
Kaplan, A., Tichatschke, R. Iterative processes for solving incorrect convex variational problems. J Glob Optim 3, 243–255 (1993). https://doi.org/10.1007/BF01096742
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/BF01096742
Key words
- Regularization
- weakly coercive variational inequalities
- semi-infinite programming problems
- numerical algorithms for convex programming problems