Abstract
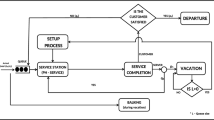
We consider aM/G/1 queue modified such that an arriving customer may be totally or partially rejected depending on a r.v. (the barricade) describing his impatience and on the state of the system. Three main variants of this scheme are studied. The steady-state distribution is expressed in terms of Volterra equations and the relation to storage processes, dams and queues with state-dependent Poisson arrival rate is discussed. For exponential service times, we further find the busy period Laplace transform in the case of a deterministic barricade, whereas for exponential barricade it is shown by a coupling argument that the busy period can be identified with a first passage time in an associated birth-death process.
Similar content being viewed by others
References
L.G. Afaneseva, Existence of a limit distribution in queueing systems with bounded sojourn time, Th. Prob. Appl. 10 (1965) 515–522.
S. Asmussen,Applied Probability and Queues (Wiley, Chichester New York, 1987).
S. Asmussen and D. Perry, On cycle maxima, first passage problems and extreme value theory for queues, Stoch. Models 8 (1992) 421–458.
S. Asmussen and M. Bladt, Phase-type distributions and risk processes with premiums dependent on the current reserve, to appear in Scand. Act. J.
C.T.H. Baker,The Numerical Solution of Integral Equations (Clarendon Press, Oxford, 1977).
F. Bacelli and A.M. Makowski, Dynamic, transient and stationary behavior of the M/G/1 queue via martingales, Ann. Prob. 17 (1989) 1691–1699.
P.P. Bhattacharya and A. Eprhremides, Stochastic monotonicity of multiserver queues with impatient customers, J. Appl. Prob. 28 (1991) 673–682.
P.P. Bhattacharya and A. Eprhemides, Optimal scheduling under strict deadlines, IEEE Trans. Autom. Control 34 (1989) 721–728.
S. Browne and K. Sigman, Work-modulated queues with applications to storage processes, J. Appl. Prob. 29 (1992) 699–712.
J.W. Cohen, Single server queue with restricted accessibility, J. Eng. Math. 3 (1969) 265–285.
J.W. Cohen,The Single Server Queue, revised ed. (North-Holland, Amsterdam, 1982).
D.J. Daley, Single server queueing system with uniformly limited queuing time, J. Aust. Math. Soc. 4 (1964) 489–505.
Gavish and P.J. Schweitzer, The Markovian queue with bounded waiting time, Man. Sci. 23 (1977) 1349–1357.
B.V. Gnedenko and I.N. Kovalenko,Introduction to Queueing Theory, 2nd Ed. (Birkhäuser, Basel, 1989).
J.M. Harrison and S.I. Resnick, The stationary distribution and first exit probabilities of a storage process with general release rule, Math. Oper. Res. 1 (1976) 347–358.
J. Keilson, A gambler's ruin type problem in queueing theory, Oper. Res. 11 (1963) 570–576.
H. Kaspi and D. Perry, Inventory systems of perishable commodities, Adv. Appl. Prob. 15 (1983) 674–685.
H. Kaspi and D. Perry, Inventory systems of perishable commodities with renewal input and Poisson output, Adv. Appl. Prob. 16 (1984) 402–421.
C. Knessl, B.J. Matowsky, Z. Schuss and C. Tier, Busy period distribution on state-dependent queues, Queing Systems 2 (1987) 285–305.
M. Loeve,Probability Theory, 3rd ed. (Van Nostrand, Princeton, 1963).
M. Miyazawa, The intensity conservation law for queues with randomly changed service rates, J. Appl. Prob. 22 (1985) 408–418.
M.F. Neuts,Matrix-Geometric Solutions in Stochastic Models (Johns Hopkins University Press, Baltimore. London, 1981).
J. Neveu,Martingales á Temps Discret (Masson, Paris, 1972).
D. Perry and M.J.M. Posner, Analysis of production/inventory systems with several production rates, Stoch. Models 6 (1990) 99–116.
W.A. Rosenkranzt, Calculation of the Laplace transform of the length of the busy period for the M/GI/1 queue via martingales, Ann. Prob. 11 (1989) 817–818.
S. Schock Petersen, Calculation of ruin probabilities when the premium depends on the current reserve, Scand. Act. J. (1988).
D. Sonderman, Comparing multi-server queues with finite waiting rooms, I, II, Appl. Prob. 11 (1979) 439–455.
D. Stoyan,Comparison Method for Queues and Other Stochastics Models (Wiley, 1983).
W. Whitt, Comparing counting processes and queues, Adv. Appl. Prob. 13 (1981) 207–220.
R.W. Wolff, An upper bound for multi-channel queues, J. Appl. Prob. 14 (1977) 884–888.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Perry, D., Asmussen, S. Rejection rules in theM/G/1 queue. Queueing Syst 19, 105–130 (1995). https://doi.org/10.1007/BF01148942
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF01148942