Abstract
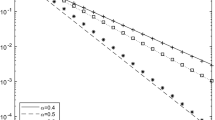
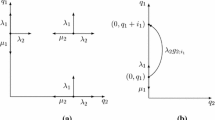
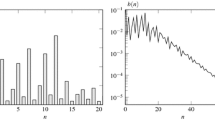
A queueing model having a nonstationary Interrupted Poisson arrival process (IPP(t)),s time-dependent exponential unreliable/repairable servers and finite capacityc is introduced, and an approximation method for analysis of it is developed and tested. Approximations are developed for the time-dependent queue length moments and the system viewpoint waiting time distributions and moments. The approximation involves state-space partitioning and numerically integrating partial-moment differential equations (PMDEs). Surrogate distribution approximations (SDA's) are used to close the system of PMDEs. The approximations allow for analysis using only (s + 1)(s + 6) differential equations for the queue length moments rather than the 2(c + 1)(s +1) equations required by the classic method of numerically integrating the full set of Kolmogorov-forward equations. Effectively hours of cpu time are reduced to minutes for even modest capacity systems. Approximations for waiting time distributions and moments are developed.
Similar content being viewed by others
References
G.M. Clark, Use of Polya distributions in approximate solutions to nonstationary M/M/s queues, Comm. ACM 24 (1981) 206–218.
R.B. Cooper,Introduction to Queueing Theory, 2nd ed. (North-Holland, Elsevier, New York, 1981).
W.K. Grassmann, Transient solutions in Markovian queueing systems, Compt. Oper. Res. 4 (1977) 47–53.
D. Gross and D. Miller, The randomization technique as a modeling tool and solution procedure for transient Markov processes, Oper. Res. 32 (1984) 362–379.
IMSL-The International Mathematical and Statistical Libraries (2500 ParkWest Tower One 2500 CityWest Boulevard Houston, TX 77042).
N.L. Johnson and S. Kotz,Urn Models and Their Applications (John Wiley & Sons, New York, 1977).
B.O. Koopman, Air terminal queues under time-dependent conditions, Oper. Res., 20 (1972) 1089–1114.
A. Kuczura, The interrupted Poisson process as an overflow process, Bell System Tech. J. 52 (1973) 437–448.
B. Melamed and M. Yadin, Randomization procedure in the computation of cumulative-time distributions over discrete state Markov processes, Oper. Res. 32 (1984) 926–943.
B. Melamed and M. Yadin, Numerical computations of sojourn-time distributions in queueing networks, J. Assoc. Comput. Mach. 31 (1984) 839–854.
J.A. Morrison, An overflow system in which queueing takes precedence, Bell System Tech. J. 60 (1981) 1–12.
M.F. Neuts,Matrix-Geometric Solutions in Stochastic Models: An Algorithmic Approach (The Johns Hopkins University Press, Baltimore MD, 1981).
K.L. Ong, Approximating nonstationary multivariate queueing models, Ph.D. dissertation, Purdue University, West Lafayette, IN, 1985.
K.L. Ong and M.R. Taaffe, Approximating nonstationary Ph(t)/Ph(t)/1/c queueing systems, Math. Comput. Simulation (1988) to appear.
S.S. Oren and M.H. Rothkopf, Ans + 1 equation closure approximation for the nonstationary M/M/s queue, ARG-82-2 Analysis Research Group, Xerox Palo Alto Research Center, Palo Alto, CA, 1982.
J.H. Rath and D. Sheng, Approximations for overflow models from queues with finite waiting rooms, Oper. Res. 27 (1979) 1208–1216.
K.L. Rider, A simple approximation to the average size in the time-dependent M/M/1 queue, J. Assoc. Comput. Mach. 23 (1976) 361–367.
M.H. Rothkopf and S.S. Oren, A closure approximation for the nonstationary M/M/s queue, Management Sci. 25 (1979) 552–534.
M.R. Taaffe, Approximating nonstationary queueing models, Ph.D. dissertation, The Ohio State University, Columbus, OH, 1982.
M.R. Taaffe and G.M. Clark. Approximating nonstationary two priority nonpreemptive queueing systems, Naval. Res. Logist 35 (1988) 125–145.
M.R. Taaffe and K.L. Ong, Approximating nonstationary Ph(t)/M(t)/s/c queueing systems, Ann. Oper. Res. 8 (1987) 103–116.
R.W. Wolff, Poisson arrivals see time averages, Oper. Res. 30 (1982) 362–379.
Author information
Authors and Affiliations
Additional information
This research was partially funded by National Science Foundation grant ECS-8404409.
Rights and permissions
About this article
Cite this article
Ong, K.L., Taaffe, M.R. Nonstationary queues with Interrrupted Poisson arrivals and unreliable/repairable servers. Queueing Syst 4, 27–46 (1989). https://doi.org/10.1007/BF01150854
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF01150854