Abstract
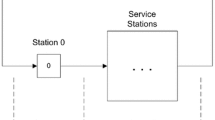
Consider a two-station queueing network with two types of jobs: type 1 jobs visit station 1 only, while type 2 jobs visit both stations in sequence. Each station has a single server. Arrival and service processes are modeled as counting processes with controllable stochastic intensities. The problem is to control the arrival and service processes, and in particular to schedule the server in station 1 among the two job types, in order to minimize a discounted cost function over an infinite time horizon. Using a stochastic intensity control approach, we establish the optimality of a specific stationary policy, and show that its value function satisfies certain properties, which lead to a switching-curve structure. We further classify the problem into six parametric cases. Based on the structural properties of the stationary policy, we establish the optimality of some simple priority rules for three of the six cases, and develop heuristic policies for the other three cases.
Similar content being viewed by others
References
M. Bartroli, On the structure of optimal control policies for networks of queues, Ph.D. Dissertation, Department of Operations Research, University of North Carolina, Chapel Hill, NC 27514 (1989).
M. Bartroli and S. Stidham, Towards a unified theory of structure of optimal policies for control of networks of queues, Technical Report, Department of Operations Research, University of North Carolina, Chapel Hill, NC 27514 (1987).
P. Brémaud,Point Processes and Queues (Springer, New York, 1981).
H. Chen, Optimal intensity control of a multi-class queue, Queueing Syst. 5 (1989) 281–294.
H. Chen and D.D. Yao, Optimal intensity control of a queueing system with state-dependent capacity limit, IEEE Trans. Auto. Contr. AC-35 (1990) 459–464.
P. Glasserman and D.D. Yao, Monotone optimal control of permutable queueing systems, Math. Oper. Res. 19 (1994) 449–476.
J.M. Harrison,Brownian Motion and Stochastic Flow Systems (Wiley, New York, 1985).
J.M. Harrison, Brownian models of queueing networks with heterogeneous customer populations, in:Stochastic Differential Systems, Stochastic Control Theory and Applications, eds. W. Fleming and P.L. Lions, IMA Vol. 10 (Springer, New York, 1988).
J.M. Harrison and L.M. Wein, Scheduling networks of queues: Heavy traffic analysis of a simple open network, Queueing Syst. 5 (1989) 265–280.
B. Hajek, Optimal control of two interacting service stations, IEEE Trans. Auto. Contr. AC-29 (1984) 491–499.
L. Li, A stochastic model of production firms, Math. Oper. Res. 13 (1988) 447–466.
Z. Rosberg, P. Varaiya and J. Walrand, Optimal control of service in tandem queues, IEEE Trans. Auto. Contr. AC-27 (1982) 600–609.
S. Ross,Stochastic Processes (Wiley, New York, 1983).
R. Serfozo, An equivalence between discrete- and continuous-time Markov decision processes, Oper. Res. 27 (1979) 616–620.
R. Serfozo, Optimal control of random walks, birth and death processes, and queues, Adv. Appl. Prob. 13 (1981) 61–83.
S. Stidham, Optimal control of admission to a queueing system, IEEE Trans. Auto. Contr. AC-30 (1985) 705–713.
S. Stidham, Scheduling, routing and flow control in stochastic networks, in:Stochastic Differential Systems, Stochastic Control Theory and Applications, eds. W. Flemming and P.L. Lions, IMA Vol. 10 (Springer, New York, 1988).
S. Stidham and R.R. Weber, Monotonic and insensitive optimal policies for control of queues with undiscounted costs, Oper. Res. 37 (1989) 611–625.
D.M. Topkis, Minimizing a submodular function on a lattice, Oper. Res. 26 (1978) 305–321.
M.H. Veatch and L.M. Wein, Monotone control of queueing and production/inventory systems, Queueing Syst. 12 (1992) 391–408.
J. Walrand,An Introduction to Queueing Networks (Prentice-Hall, Englewood Cliffs, NJ, 1988).
R.R. Weber and S. Stidham, Optimal control of service rates in network of queues, Adv. Appl. Prob. 19 (1987) 202–218.
L.M. Wein, Optimal control of a two-station Brownian network, Math. Oper. Res. 15 (1990) 215–242.
L.M. Wein, Scheduling networks of queues: Heavy traffic analysis of a two-station network with controllable inputs, Oper. Res. 38 (1990) 1065–1078.
P. Whittle,Optimization Over Time (Wiley, New York, 1983).
P. Yang, Pathwise solutions for a class of linear stochastic systems, Ph.D. Dissertation, Department of Operations Research, Stanford University, Stanford, CA (1988).
A.A. Yushkevich, Controlled Markov models with countable state space and continuous time, Theory Prob. Appl. 22 (1977) 215–235.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Chen, H., Yang, P. & Yao, D.D. Control and scheduling in a two-station queueing network: Optimal policies and heuristics. Queueing Syst 18, 301–332 (1994). https://doi.org/10.1007/BF01158766
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF01158766