Abstract
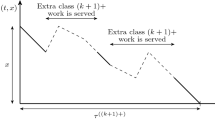
In this note we consider the fluid queue driven by anM/M/1 queue as analysed by Virtamo and Norros [Queueing Systems 16 (1994) 373–386]. We show that the stationary buffer content in this model can be easily analysed by looking at embedded time points. This approach gives the stationary buffer content distribution in terms of the modified Bessel function of the first kind of order one. By using a suitable integral representation for this Bessel function we show that our results coincide with the ones of Virtamo and Norros.
Similar content being viewed by others
References
M.A. Abramowitz and I.A. Stegun (eds.),Handbook of Mathematical Functions (Dover, New York, 1972).
D.P. Gaver and R.G. Miller, Limiting distributions for some storage problems, in:Studies in Applied Probability and Management Science, eds. K.J. Arrow, S. Karlin and H. Scarf (Stanford University Press, Stanford, 1962) pp. 110–126.
O. Kella and W. Whitt, A storage model with a two-state random environment, Oper. Res. 40 (1992) S257-S262.
L. Kleinrock,Queueing Systems, Vol. I: Theory (Wiley, New York, 1975).
J. Virtamo and I. Norros, Fluid queue driven by anM/M/1 queue, Queueing Systems 16 (1994) 373–386.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Adan, I., Resing, J. Simple analysis of a fluid queue driven by an M/M/1 queue. Queueing Syst 22, 171–174 (1996). https://doi.org/10.1007/BF01159399
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF01159399