Algorithms for projecting points to give the most uniform distribution with applications to hashing

Abstract

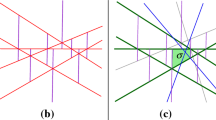
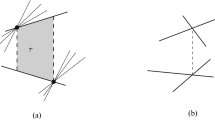
This paper presents several algorithms for projecting points so as to give the most uniform distribution. Givenn points in the plane and an integerb, the problem is to find an optimal angleθ ofb equally spaced parallel lines such that points are distributed most uniformly over buckets (regions bounded by two consecutive lines). An algorithm is known only in thetight case in which the two extreme lines are the supporting lines of the point set. The algorithm requiresO(bn² logn) time and On²+bn) space to find an optimal solution. In this paper we improve the algorithm both in time and space, based on duality transformation. Two linear-space algorithms are presented. One runs in On²+K log n+bn) time, whereK is the number of intersections in the transformed plane.K is shown to beO(@#@ n²+bn@#@) based on a new counting scheme. The other algorithm is advantageous ifb < √n. It performs a simplex range search in each slab to enumerate all the lines that intersectbucket lines, and runs in O(b^0.610n^1.695+K logn) time. It is also shown that the problem can be solved in polynomial time even in therelaxed case. Its one-dimensional analogue is especially related to the design of an optimal hash function for a static set of keys.