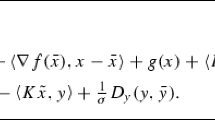Skip to main content
SpringerLink
Log in

Applications of a general convergence theory for outer approximation algorithms

  • Published:
Mathematical Programming Submit manuscript

Abstract

Eaves and Zangwill [2] have developed a very general theory of the convergence of cutting plane algorithms. This theory is applied to prove the convergence of Geoffrion's Generalized Benders Decomposition procedure (GBD) [5]. Using the insight provided by the general theory, GBD is then modified to permit the deletion of old constraints without upsetting the infinite convergence property. Finally, certain approximations of GBD are presented and the robustness of the convergence results is indicated.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. C. Berge,Topological spaces (MacMillan, New York, 1963).

    Google Scholar 

  2. B.C. Eaves and W.I. Zangwill, “Generalized cutting plane algorithms”,SIAM Journal on Control 9 (4) (1971) 529–542.

    Google Scholar 

  3. A.M. Geoffrion, “Primal resource-directive approaches for optimizing nonlinear decomposable systems”,Operations Research 18 (3) (1970) 375–403.

    Google Scholar 

  4. A.M. Geoffrion, “Elements of large scale mathematical programming, Parts I and II”,Management Science 16 (11) (1970) 652–691.

    Google Scholar 

  5. A.M. Geoffrion, “Generalized Benders Decomposition”, Working Paper No. 159, Western Management Science Institute, University of California, Los Angeles, Calif. (April 1970; revised September 1970);Journal of Optimization Theory and Applications, to appear.

    Google Scholar 

  6. A.M. Geoffrion, “Vector maximal decomposition programming”, Working Paper No. 164, Western Management Science Institute, University of California, Los Angeles, Calif. (September 1970).

    Google Scholar 

  7. F. Hausdorff,Set theory (Chelsea, New York, 1962).

    Google Scholar 

  8. W.W. Hogan, “Point-to-set maps in mathematical programming”,SIAM Review 15 (3) (1973).

  9. R. Meyer, “The validity of a family of optimization methods”,SIAM Journal on Control 8 (1) (1970) 41–54.

    Google Scholar 

  10. R.T. Rockafellar,Convex analysis (Princeton University Press, Princeton, N.J., 1970).

    Google Scholar 

  11. D.M. Topkis, “Cutting-plane methods without nested constraint sets”,Operations Research 18 (3) (1970) 404–413.

    Google Scholar 

  12. D.M. Topkis, “A note on cutting plane methods without nested constraint sets”,Operations Research 18 (6) (1970) 1216–1220.

    Google Scholar 

  13. D.M. Topkis and A.F. Veinott, Jr., “On the convergence of some feasible directions algorithms for nonlinear programming”,SIAM Journal on Control 5 (2) (1967) 268–279.

    Google Scholar 

  14. W.I. Zangwill,Nonlinear programming (Prentice-Hall, Englewood Cliffs, N.J., 1969).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Interior, Office of Energy Data and Analysis, Washington, D.C., USA

    William W. Hogan

Authors
  1. William W. Hogan
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

This research was supported by the National Science Foundation under Grant GP-22108.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Hogan, W.W. Applications of a general convergence theory for outer approximation algorithms. Mathematical Programming 5, 151–168 (1973). https://doi.org/10.1007/BF01580118

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF01580118

Keywords

Search

Navigation