Abstract
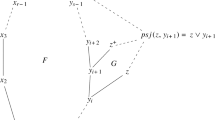
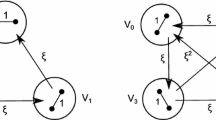
For a bimatrix game one may visualize two bounded polyhedronsX andY, one for each player. OnX × Y one may visualize, as a graphG, the set of almost-complementary points (see text).\(\bar G\) consists of an even number of nodes, one for each complementary point (one for the origin, others corresponding to extreme points which are equilibrium points); arcs (extreme point paths of almost complementary points); and possibly loops (paths with no equilibrium points).
Shapley has shown that one may assign indices (+) and (−) to nodes, and directions called (+) and (−) to arcs or loops in such a way that, leaving a (+) node one moves always in a (+) direction, terminating at a (−) node. Indices and directions for a point are determined knowing only the point.
In this paper, these concepts are generalized to labelled pseudomanifolds. An integer labelling of the vertices identifies theG-set of almost-completely labelled simplexes. It is shown that in order for theG-set of any labelling to be directed as above it is necessary and sufficient that the pseudomanifold be orientable.
Realized examples for situations of current interest are also developed.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
P. Alexandroff,Elementary concepts of topology Translated by A.N. Obolensky (Ungar Publishing Co., New York, 1965).
B.C. Eaves, “An odd theorem”,Proceedings of the American Mathematical Society 26 (3) (1970) 509–513.
B.C. Eaves and H. Scarf, “The solution of systems of piecewise linear equations”,Mathematics of Operations Research, to appear.
Ky Fan, “Simplicial maps from an orientablen-pseudomanifold intoS m with octahedral triangulation”,Journal of Combinatorial Theory 2 (1967) 588–602.
C.B. Garcia, “A hybrid algorithm for the computation of fixed points”, Techn. Rept. #150, Dept. pf Math. Sci., Clemson University (sept. 1973).
C.B. Garcia, C.E. Lemke and H.-J. Lüthi, “Simplicial approximation of an equilibrium point for non-cooperativeN-person games” in: T.C. Hu and S.M. Robinson, eds.,Mathematical programming (Academic Press, New York, 1973) 227–260.
H.W. Kuhn, “Systematic search on pseudomanifolds”, to appear.
H.W. Kuhn, “Simplicial approximation of fixed points”,Proceedings of the national academy of science 61 (1968) 1238–1242.
H.W. Kuhn, “A new proof of the fundamental theorem of algebra”,Mathematical Programming Study 1 (1974) 148–158.
C.E. Lemke, “Recent results on complementarity problems”, in: J.B. Rosen, O.L. Mangasarian and K. Ritter, eds.,Nonlinear Programming (Academic Press, New York, 1968) 349–384.
H.E. Scarf, “The approximation of fixed points of a continuous mapping”,SIAM Journal of Applied Mathematics 15 (1967) 1328–1343.
L.S. Shapley, “A note on the Lemke—Howson algorithm”,Mathematical Programming Study 1 (1974) 175–189.
L.S. Shapley, “On balanced games wihtout side payments”, in: T.C. Hu and S.M. Robinson, eds.,Mathematical programming (Academic Press, New York, 1973) 261–290.
Author information
Authors and Affiliations
Additional information
This research was supported by the National Science Foundation Grant NSF GP-32844X.
Rights and permissions
About this article
Cite this article
Lemke, C.E., Grotzinger, S.J. On generalizing shapley's index theory to labelled pseudomanifolds. Mathematical Programming 10, 245–262 (1976). https://doi.org/10.1007/BF01580670
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/BF01580670