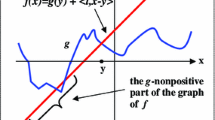
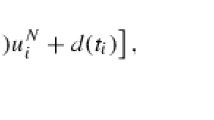Abstract
This paper deals with a continuous time, subgradient projection algorithm, shown to generate trajectories that accumulate to the solution set. Under a strong convexity assumption we show that convergence is exponential in norm. A sharpness condition yields convergence in finite time, and the necessary lapse is estimated. Invoking a constraint qualification and a non-degeneracy assumption, we demonstrate that optimally active constraints are identified in finite time.
Similar content being viewed by others
References
A.S. Antipin, “Neprerivnie i iterativnie proctcecci c opertorami proektirovania i tipa proektirvanija” (“Continuous and iterative processes using projection and projection type operators”),Voprosy Kibernetiki (Moscow) (1989) 5–43.
A.S. Antipin, “Gradient and proximal continuous controllable processes,” working paper, private communication (1989).
J.P. Aubin and A. Cellina,Differential Inclusions (Springer, Berlin, 1984).
D. Bertsekas, “On the Goldstein—Levitin—Polyak gradient projection method,”IEEE Transactions on Automatic Control 21 (1976) 174–184.
J.V. Burke and J.J. Moré, “On the identification of active constraints,” Technical Report 86-82, Department of Mathematics and Computer Science, Argonne National Laboratory (Argonne, IL, 1986).
J.V. Burke, “On the identification of active constraints II: The nonconvex case,” Department of Mathematics, University of Washington, manuscript (Seattle, WA, 1988).
P.H. Calamai and J.J. Moré, “Projected gradient methods for linearly constrained problems,”Mathematical Programming 39 (1987) 93–116.
J.C. Dunn, “Global and asymptotic convergence rate estimates for a class of projected gradient processes,”SIAM Journal on Control and Optimization 19 (1981) 368–400.
Yu.G. Evtushenko and V.G. Zhadan, “Application of the method of Luapunov functions to the study of convergence of numerical methods,”USSR Computational Mathematics and Mathematical Physics 15 (1975) 96–100.
Yu.G. Evtushenko,Numerical Optimization Techniques (Optimization software, New York, 1985).
S.D. Flåm and A. Ben-Israel, “Approximating saddle points as equilibria of differential inclusions,”Journal of Mathematical Analysis and Applications 141 (1989) 264–277.
S.D. Flåm and A. Ben-Israel, “A continuous approach to oligopolistic market equilibrium,”Operations Research 38 (1990) 1045–1051.
A.A. Goldstein, “Convex programming in Hilbert space,”Bulletin of the American Mathematical Society 70 (1984) 709–710.
F.J. Gould and J.W. Tolle, “A necessary and sufficient constraint qualification for constrained optimization,”SIAM Journal on Applied Mathematics 20 (1971) 164–172.
M. Guignard, “Generalized Kuhn-Tucker conditions for mathematical programming in a Banach space,”SIAM Journal on Control and Optimization 7 (1969) 232–241.
E.S. Levitin and B.T. Polyak, “Constrained minimization problems,”USSR Computational Mathematics and Mathematical Physics 6 (1966) 1–50.
G.P. McCormick and R.A. Tapai, “The gradient projection method under mild differentiability assumptions,”SIAM Journal on Control and Optimization 10 (1972) 93–98.
R.R. Phelps, “Openness of the metric projection in certain Banach spaces,”Journal of Approximation Theory 42 (1984) 70–79.
R.R. Phelps, “Metric projection and the gradient projection method in Banach spaces,”SIAM Journal on Control and Optimization 23 (1985) 973–977.
R.R. Phelps, “The gradient projection method using Curry's steplength,”SIAM Journal on Control and Optimization 24 (1986) 692–699.
B.T. Polyak,Introduction to Optimization (Optimization software, New York, 1987).
N.Z. Shor,Minimization Methods for Non-differentiable Functions (Springer, Berlin, 1985).
V.I. Venets and M.V. Rybashov, “The method of Lyapunov in the study of continuous algorithms of mathematical programming,”USSR Computational Mathematics and Mathematical Physics 17 (1977) 64–77.
V.I. Venets, “Stability of continuous algorithms for solving convex constrained minimization problems using projection onto the feasible set,”Automation and Remote Control 44 (1983) 18–23.
V.I. Venets, “Continuous algorithms for solution of convex constrained minimization problems and finding saddle points of convex-concave functions with the use of projection operators,”Optimization 16 (1985) 519–533.
E.H. Zarantonello, “Projections on convex sets in Hilbert space and spectral theory,” in: E.H. Zarantonello, ed.,Contributions to Nonlinear Functional Analysis (Academic Press, New York, 1971).
Author information
Authors and Affiliations
Additional information
This research has been partially supported by Rutgers University, RUTCOR, New Brunswick, NJ 08903, USA, and by the Memorial Fund of Wilhelm Kheilhau.
Rights and permissions
About this article
Cite this article
Flåm, S.D. On finite convergence and constraint identification of subgradient projection methods. Mathematical Programming 57, 427–437 (1992). https://doi.org/10.1007/BF01581092
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF01581092