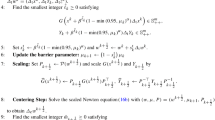Skip to main content
SpringerLink
Log in

A globally convergent primal—dual interior point algorithm for convex programming

  • Published:
Mathematical Programming Submit manuscript

Abstract

In this paper, we study the global convergence of a large class of primal—dual interior point algorithms for solving the linearly constrained convex programming problem. The algorithms in this class decrease the value of a primal—dual potential function and hence belong to the class of so-called potential reduction algorithms. An inexact line search based on Armijo stepsize rule is used to compute the stepsize. The directions used by the algorithms are the same as the ones used in primal—dual path following and potential reduction algorithms and a very mild condition on the choice of the “centering parameter” is assumed. The algorithms always keep primal and dual feasibility and, in contrast to the polynomial potential reduction algorithms, they do not need to drive the value of the potential function towards — ∞ in order to converge. One of the techniques used in the convergence analysis of these algorithms has its root in nonlinear unconstrained optimization theory.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. D.P. Bertsekas,Constrained Optimization and Lagrange Multiplier Methods (Academic Press, London, 1982).

    Google Scholar 

  2. R.S. Dembo, “Dual to primal conversion in geometric programming,”Mathematical Programming 26 (1978) 243–252.

    Google Scholar 

  3. I.I. Dikin, “Iterative solution of problems of linear and quadratic programming,”Soviet Mathematics Doklady 8 (1967) 674–675.

    Google Scholar 

  4. D.-Z. Du and X.-S Zhang, “Global convergence of Rosen's gradient projection method,”Mathematical Programming 44 (1989) 357–366.

    Google Scholar 

  5. R. Fletcher,Practical Methods of Optimization (Wiley, New York, 1987).

    Google Scholar 

  6. C.C. Gonzaga, “An algorithm for solving linear programming problems in O (n 3 L) operations,” in: N. Megiddo, ed.,Progress in Mathematical Programming: Interior Point Algorithms and Related Methods (Springer, New York, 1989) pp. 1–28.

    Google Scholar 

  7. O. Guler, “Existence of interior points and interior paths in nonlinear monotone complementarity problems,”Mathematics of Operations Research 18 (1993) 128–147.

    Google Scholar 

  8. D. den Hertog, C. Roos and T. Terlaky, “On the classical logarithmic barrier function method for a class of smooth convex programming problems,”Journal of Optimization Theory and Applications 73 (1992) 1–25.

    Google Scholar 

  9. D. den Hertog, C. Roos and T. Terlaky, “A large-step analytic center method for a class of smooth convex programming problems”,SIAM Journal on Optimization 2 (1992) 55–70.

    Google Scholar 

  10. F. Jarre, G. Sonnevend and J. Stoer, “On the complexity of a numerical algorithm for solving generalized convex quadratic programs by following a central path, in: J.C. Lagarias and M.J. Todd, editors,Mathematical Developments Arising from Linear Programming: Proceedings of a Joint Summer Research Conference held at Bowdoin College, Brunswick, Maine, USA, June/July 1988, volume 114 ofContemporary Mathematics (American Mathematical Society, Providence, Rhode Island, USA, 1990) pp. 233–242.

    Google Scholar 

  11. N. Karmarkar, “A new polynomial time algorithm for linear programming,”Combinatorica 4 (1984) 373–395.

    Google Scholar 

  12. M. Kojima, N. Megiddo and S. Mizuno, “Theoretical convergence of large-step primal—dual interior point algorithms for linear programming,”Mathematical Programming 59 (1993) 1–21.

    Google Scholar 

  13. M. Kojima, N. Megiddo and T. Noma, “Homotopy continuation methods for nonlinear complementarity problems,”Mathematics of Operations Research 16 (1991) 754–774.

    Google Scholar 

  14. M. Kojima, N. Megiddo, T. Noma and A. Yoshise, “A unified approach to interior point algorithms for linear complementarity problems,” in:Lecture Notes in Computer Science No. 538 (Springer, Berlin, 1991).

    Google Scholar 

  15. M. Kojima, S. Mizuno and T. Noma, “Limiting behavior of trajectories generated by a continuation method for monotone complementarity problems,”Mathematics of Operations Research 15 (1990) 662–675.

    Google Scholar 

  16. M. Kojima, S. Mizuno and A. Yoshise, “A polynomial-time algorithm for a class of linear complementarity problems,”Mathematical Programming 44 (1989) 1–26.

    Google Scholar 

  17. M. Kojima, S. Mizuno and A. Yoshise, “A primal-dual interior point algorithm for linear programming,” in: N. Megiddo, ed.,Progress in Mathematical Programming: Interior Point Algorithms and Related Methods (Springer, New York, 1989) pp. 131–158.

    Google Scholar 

  18. M. Kojima, S. Mizuno and A. Yoshise, “An O(√nL) iteration potential reduction algorithm for linear complementarity problems,” Mathematical Programming 50 (1991) 331–342.

    Google Scholar 

  19. K.O. Kortanek, F. Potra and Y. Ye, “On some efficient interior point methods for nonlinear convex programming,”Linear Algebra and its Applications 152 (1991) 169–189.

    Google Scholar 

  20. K.O. Kortanek and J. Zhu, “A polynomial barrier algorithm for linearly constrained convex programming problems,”Mathematics of Operations Research 18 (1993) 116–127.

    Google Scholar 

  21. L. McLinden, “The complementarity problem for maximal monotone multifunctions,” in: R.W. Cottle, F. Giannessi and J.-L. Lions, eds.,Variational Inequalities and Complementarity Problems (Wiley, New York, 1980) pp. 251–270.

    Google Scholar 

  22. N. Megiddo, “Pathways to the optimal set in linear programming,” in: N. Megiddo, ed.,Progress in Mathematical Programming: Interior Point Algorithms and Related Methods (Springer, New York, 1989) pp. 131–158.

    Google Scholar 

  23. S. Mehrotra and J. Sun, “An interior point algorithm for solving smooth convex programs based on Newton's method,” in: J.C. Lagarias and M.J. Todd, ed.,Contemporary Mathematics: Proceedings of the AMS—IMS—SIAM Joint Summer Research Conference on “Mathematical Developments Arising from Linear Programming”, held at Bowdoin College, Brunswick, Maine on July 25–31, 1988, vol. 114 (AMS, Province, RI, 1990) pp. 265–284.

    Google Scholar 

  24. S. Mizuno, M.J. Todd and Y. Ye, “On adaptive step primal-dual interior-point algorithms for linear programming,”Mathematics of Operations Research 18 (1993) 945–981.

    Google Scholar 

  25. S. Mizuno, A. Yoshise and T. Kikuchi, “Practical polynomial time algorithms for linear complementarity problems,”Journal of the Operations Research Society of Japan 32 (1989) 75–92.

    Google Scholar 

  26. R.D.C. Monteiro and I. Adler, “Interior path following primal—dual algorithms. Part II: Convex quadratic programming,”Mathematical Programming 44 (1989) 43–66.

    Google Scholar 

  27. R.D.C. Monteiro and I. Adler, “Interior path following primal—dual algorithms. Part I: Linear programming,”Mathematical Programming 44 (1989) 27–41.

    Google Scholar 

  28. R.D.C. Monteiro and I. Adler, “An extension of kamarkar type algorithm to a class of convex separable programming problems with global linear rate of convergence,”Mathematics of Operations Research 15 (1990) 408–422.

    Google Scholar 

  29. R.D.C. Monteiro, I. Adler and Mauricio G.C. Resende, “A polynomial-time primal—dual affine scaling algorithm for linear and convex quadratic programming and its power series extension,”Mathematics of Operations Research 15 (1990) 191–214.

    Google Scholar 

  30. J.J. Moré, “Class of functions and feasibility conditions in nonlinear complementarity problem,”Mathematical Programming 6 (1974) 327–338.

    Google Scholar 

  31. Y.E. Nesterov and A.S. Nemirovsky, “A general approach to the design of optimal methods for smooth convex functions minimization,”Ekonomika i Matem. Metody 24 (1988) 509–517. (In Russian; English transl. Matekon: Translations of Russian and East European Math. Economics.)

    Google Scholar 

  32. J.S. Pang, “Iterative descent methods for a row sufficient linear complementarity problem,”SIAM Journal on Matrix Analysis and Applications 12 (1991) 611–624.

    Google Scholar 

  33. J. Renegar, “A polynomial-time algorithm based on Newton's method for linear programming,”Mathematical Programming 40 (1988) 59–93.

    Google Scholar 

  34. R.T. Rockafellar,Convex Analysis (Princeton University Press, Princeton, NJ, 1970).

    Google Scholar 

  35. G. Sonnevend, “An analytical centre for polyhedrons and new classes of global algorithms for linear (smooth, convex) programming,” in: A. Prekopa, ed.,Lecture Notes in Control and Information Sciences, No. 84 (Springer, Berlin, 1985) pp. 866–876.

    Google Scholar 

  36. K. Tanabe, “Complementarity-enforcing centered Newton method for mathematical programing: global theory,” in: K. Tone, ed.,New Methods for Linear Programming (The Institute of Statistical Mathematics, Tokyo, 1987) pp. 118–144.

    Google Scholar 

  37. K. Tanabe, “Centered Newton method for mathematical programming,” in: M. Iri and K. Yajima, eds.,Systems Modelling and Optimization (Springer, New York, 1988) pp. 197–206.

    Google Scholar 

  38. M.J. Todd and Y. Ye, “A centered projective algorithm for linear programming,”Mathematics of Operations Research 15 (1990) 508–529.

    Google Scholar 

  39. P. Tseng, “Global linear convergence of a path following algorithm for some monotone variational inequality problems.”Journal of Optimization Theory and Applications. 75 (1992) 265–279.

    Google Scholar 

  40. P.M. Vaidya, “An algorithm for linear programming which requires O((m + n)n 2 +(m + n)L) arithmetic operations,”Mathematical Programming 47 (1990) 175–202.

    Google Scholar 

  41. Y. Ye, “An O(n 3 L) potential reduction algorithm for linear programmig,”Mathematical Programming 50 (1991) 239–258.

    Google Scholar 

  42. F.A. Potra and Y. Ye, A quadratically convergent polynomial algorithm for solving entropy optimization problems,SIAM Journal on Optimization 3 (1993) 843–861.

    Google Scholar 

  43. J. Zhu, “A path following algorithm for a class of convex programming problems,”ZOR — Methods and Models of Operations Research 36 (1992) 359–377.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Systems and Industrial Engineering Department, University of Arizona, 85721, Tucson, AZ, USA

    Renato D. C. Monteiro

Authors
  1. Renato D. C. Monteiro
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Research supported in part by NSF Grant DDM-9109404.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Monteiro, R.D.C. A globally convergent primal—dual interior point algorithm for convex programming. Mathematical Programming 64, 123–147 (1994). https://doi.org/10.1007/BF01582568

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF01582568

AMS 1980 Subject Classification

Keywords

Search

Navigation