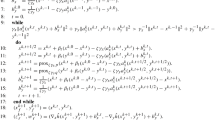Skip to main content
SpringerLink
Log in

An O(n 3 L) potential reduction algorithm for linear programming

  • Published:
Mathematical Programming Submit manuscript

Abstract

We describe a primal-dual potential function for linear programming:

$$\phi (x,s) = \rho \ln (x^T s) - \sum\limits_{j = 1}^n {\ln (x_j s_j )} $$

whereρ⩾ n, x is the primal variable, ands is the dual-slack variable. As a result, we develop an interior point algorithm seeking reductions in the potential function with\(\rho = n + \sqrt n \). Neither tracing the central path nor using the projective transformation, the algorithm converges to the optimal solution set in\(O(\sqrt n L)\) iterations and uses O(n 3 L) total arithmetic operations. We also suggest a practical approach to implementing the algorithm.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. I. Adler, N. Karmarkar, M.G.C. Resende and G. Veiga, “An implementation of Karmarkar's algorithm for linear programming,”Mathematical Programming 44 (1989) 297–335.

    Google Scholar 

  2. K.M. Anstreicher, “A monotonic projective algorithm for fractional linear programming,”Algorithmica 1 (1986) 483–498.

    Google Scholar 

  3. E.R. Barnes, “A variation on Karmarkar's algorithm for solving linear programming problems,”Mathematical Programming 36 (1986) 174–182.

    Google Scholar 

  4. D.A. Bayer and J.C. Lagarias, “The nonlinear geometry of linear programming: I. Affine and projective scaling trajectories, II. Legendre transform coordinates and central trajectories,”Transactions of the American Mathematical Society 314 (1989) 499–581.

    Google Scholar 

  5. M. Ben Daya and C.M. Shetty, “Polynomial barrier function algorithms for convex quadratic programming,” Report J 88-5, School of ISE, Georgia Institute of Technology (Atlanta, GA, 1988).

    Google Scholar 

  6. G.B. Dantzig,Linear Programming and Extensions (Princeton University Press, Princeton, NJ, 1963).

    Google Scholar 

  7. I.I. Dikin, “Iterative solution of problems of linear and quadratic programming,”Soviet Mathematics Doklady 8 (1967) 674–675.

    Google Scholar 

  8. A.V. Fiacco and G.P. McCormick,Nonlinear Programming: Sequential Unconstrained Minimization Techniques (Wiley, New York, NY, 1968).

    Google Scholar 

  9. K.R. Frisch, “The logarithmic potential method of convex programming,” Technical Report, University Institute of Economics (Oslo, Norway, 1955).

    Google Scholar 

  10. D.M. Gay, “A variant of Karmarkar's linear programming algorithm for problems in standard form,”Mathematical Programming 37 (1987) 81–90.

    Google Scholar 

  11. G. de Ghellinck and J.-P. Vial, “A polynomial Newton method for linear programming,”Algorithmica 1 (1986) 425–454.

    Google Scholar 

  12. P.E. Gill, W. Murray, M.A. Saunders, J.A. Tomlin and M.H. Wright, “On projected Newton barrier methods for linear programming and an equivalence to Karmarkar's projective method,”Mathematical Programming 36 (1986) 183–209.

    Google Scholar 

  13. D. Goldfarb and S. Liu, “An O(n 3 L) primal interior point algorithm for convex quadratic programming,” Technical Report, Department of IEOR, Columbia University (New York, NY, 1988).

    Google Scholar 

  14. C.C. Gonzaga, “Polynomial affine algorithms for linear programming,”Mathematical Programming 49 (1991) 7–21.

    Google Scholar 

  15. C.C. Gonzaga, “An algorithm for solving linear programming problems in O(n 3 L) operations,” in: N. Megiddo, ed.,Progress in Mathematical Programming, Interior Point and Related Methods (Springer, New York, 1988) pp. 1–28.

    Google Scholar 

  16. M. Iri and H. Imai, “A multiplicative barrier function method for linear programming,”Algorithmica 1 (1986) 455–482.

    Google Scholar 

  17. N. Karmarkar, “A new polynomial-time algorithm for linear programming,”Combinatorica 4 (1984) 373–395.

    Google Scholar 

  18. M. Kojima, S. Mizuno and A. Yoshise, “A polynomial-time algorithm for a class of linear complementarity problems,”Mathematical Programming 44 (1989) 1–26.

    Google Scholar 

  19. K.O. Kortanek and M. Shi, “Convergence results and numerical experiments on a linear programming hybrid algorithm,”European Journal of Operations Research 32 (1987) 47–61.

    Google Scholar 

  20. K.A. McShane, C.L. Monma and D.F. Shanno, “An implementation of a primal-dual interior point method for linear programming,”ORSA Journal on Computing 1 (1989) 70–83.

    Google Scholar 

  21. N. Megiddo, “Pathways to the optimal set in linear programming,” in: N. Megiddo, ed.,Progress in Mathematical Programming, Interior Point and Related Methods (Springer, New York, 1988) 131–158.

    Google Scholar 

  22. N. Megiddo and M. Shub, “Boundary behavior of interior point algorithms in linear programming,”Mathematics of Operations Research 14 (1989) 97–146.

    Google Scholar 

  23. S. Mehrotra and J. Sun, “An algorithm for convex quadratic programming that requires O(n 3.5 L) arithmetic operations,”Mathematics of Operations Research 15 (1990) 342–363.

    Google Scholar 

  24. C.L. Monma and A.J. Morton, “Computational experimental with a dual affine variant of Karmarkar's method for linear programming,” Technical Report, Bell Communications Research (Morristown, NJ, 1987).

    Google Scholar 

  25. R.C. Monteiro, I. Adler and M.C. Resende, “A polynomial-time primal-dual affine scaling algorithm for linear and convex quadratic programming and its power series extension,”Mathematics of Operations Research 15 (1990) 191–214.

    Google Scholar 

  26. R.C. Monteiro and I. Adler, “Interior path following primal-dual algorithms. Part I: Linear programming,”Mathematical Programming 44 (1989) 27–42.

    Google Scholar 

  27. J. Renegar, “A polynomial-time algorithm, based on Newton's method, for linear programming,”Mathematical Programming 40 (1988) 59–93.

    Google Scholar 

  28. D.F. Shanno, “Computing Karmarkar projection quickly,”Mathematical Programming 41 (1988) 61–71.

    Google Scholar 

  29. G. Sonnevend, “An analytical center for polyhedrons and new classes of global algorithms for linear (smooth, convex) programming,” in:Lecture Notes in Control and Information Sciences No. 84 (Springer, New York, 1985) pp. 866–876.

    Google Scholar 

  30. M.J. Todd and B.P. Burrell, “An extension of Karmarkar's algorithm for linear programming using dual variables,”Algorithmica 1 (1986) 409–424.

    Google Scholar 

  31. M.J. Todd and Y. Ye, “A centered projective algorithm for linear programming,”Mathematics of Operations Research 15 (1990) 508–529.

    Google Scholar 

  32. P.M. Vaidya, “An algorithm for linear programming which requires O((m+n)n 2+(m+n) 1.5 n)L) arithmetic operations,”Mathematical Programming 47 (1990) 175–201.

    Google Scholar 

  33. R.J. Vanderbei and J.C. Lagarias, “I.I. Dikin's convergence result for the affine-scaling algorithm,” manuscript, AT&T Bell Laboratories (Murray Hill, NJ, 1988).

    Google Scholar 

  34. R.J. Vanderbei, M.S. Meketon and B.A. Freedman, “On a modification of Karmarkar's linear programming algorithm,”Algorithmica 1 (1986) 395–407.

    Google Scholar 

  35. Y. Ye, “Interior algorithms for linear, quadratic, and linearly constrained convex programming,” Ph.D. Thesis, Department of Engineering-Economic Systems, Stanford Universty (Stanford, CA, 1987).

    Google Scholar 

  36. Y. Ye and M. Kojima, “Recovering optimal dual solutions in Karmarkar's polynomial algorithm for linear programming,”Mathematical Programming 39 (1987) 305–317.

    Google Scholar 

  37. Y. Ye and M.J. Todd, “Containing and shrinking ellipsoids in the path-following algorithm,”Mathematical Programming 47 (1990) 1–9.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Management Sciences, The University of Iowa, 52242, Iowa City, IA, USA

    Yinyu Ye

Authors
  1. Yinyu Ye
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Ye, Y. An O(n 3 L) potential reduction algorithm for linear programming. Mathematical Programming 50, 239–258 (1991). https://doi.org/10.1007/BF01594937

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF01594937

Key words

Search

Navigation