Skip to main content

Advertisement

Springer Nature Link
Log in

Minimum-link paths among obstacles in the plane

  • Published:
Algorithmica Aims and scope Submit manuscript

Abstract

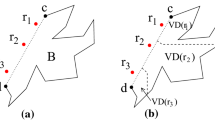
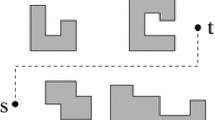
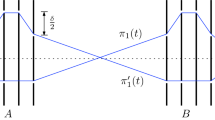
Given a set of nonintersecting polygonal obstacles in the plane, thelink distance between two pointss andt is the minimum number of edges required to form a polygonal path connectings tot that avoids all obstacles. We present an algorithm that computes the link distance (and a corresponding minimum-link path) between two points in timeO(Eα(n) log2 n) (and spaceO(E)), wheren is the total number of edges of the obstacles,E is the size of the visibility graph, and α(n) denotes the extremely slowly growing inverse of Ackermann's function. We show how to extend our method to allow computation of a tree (rooted ats) of minimum-link paths froms to all obstacle vertices. This leads to a method of solving the query version of our problem (for query pointst).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. P. K. Agarwal, Intersection and Decomposition Algorithms for Arrangements of Curves in the Plane, Ph.D. Dissertation, Robotics Report No. 207, Department of Computer Science, New York University, August 1989.

  2. M. Ben-Or, Lower bounds for algebraic computation trees,Proc. 15th ACM Symposium on the Theory of Computing, 1983, pp. 80–86.

  3. J. Canny and J. Reif, New lower bound techniques for robot motion planning and real geometry,Proc. 28th IEEE Symposium on the Foundations of Computer Science, 1987, pp. 39–48.

  4. B. Chazelle, Triangulating a simple polygon in linear time,Discrete Comput. Geom. 6 (1991), 485–524.

    Article  MATH  MathSciNet  Google Scholar 

  5. B. Chazelle and H. Edelsbrunner, An optimal algorithm for intersecting line segments in the plane,J. Assoc. Comput. Mach. 39 (1992), 1–54.

    MATH  MathSciNet  Google Scholar 

  6. H. N. Djidjev, A. Lingas, and J. Sack, AnO(n logn) algorithm for computing the link center of a simple polygon,Proc. 6th Annual Symposium on the Theoretical Aspects of Computer Science, Paderborn, February 1989, eds. B. Monien and R. Cori, Lecture Notes in Computer Science, Vol. 349, Springer-Verlag, Berlin, 1989, pp. 96–107. To appear inDiscrete Comput. Geom.

    Google Scholar 

  7. C. Ó'Dúnlaing, A tight lower bound for the complexity of path-planning for a disc,Inform. Process. Lett. 28 (1988), 165–170.

    Article  MATH  MathSciNet  Google Scholar 

  8. H. Edelsbrunner, L. J. Guibas, and M. Sharir, The complexity and construction of many faces in arrangements of lines and of segments,Discrete Comput. Geom. 5 (1990), 161–196.

    Article  MATH  MathSciNet  Google Scholar 

  9. H. Edelsbrunner, L. J. Guibas, and J. Stolfi, Optimal point location in a monotone subdivision,SIAM J. Comput. 15 (1986), 317–340.

    Article  MATH  MathSciNet  Google Scholar 

  10. H. A. El Gindy and D. Avis, A linear algorithm for computing the visibility polygon from a point,J. Algorithms 2 (1981), 186–197.

    Article  MATH  MathSciNet  Google Scholar 

  11. S. K. Ghosh and D. M. Mount, An output-sensitive algorithm for computing visibility graphs,SIAM J. Comput. 20 (1991), 888–910.

    Article  MATH  MathSciNet  Google Scholar 

  12. S. Hart and M. Sharir, Nonlinearity of Davenport-Schinzel sequences and of generalized path compression schemes,Combinatorica 6 (1986), 151–177.

    Article  MATH  MathSciNet  Google Scholar 

  13. B. Joe and R. B. Simpson, Correction to Lee's visibility polygon algorithm,BIT 27 (1987), 458–473.

    Article  MATH  Google Scholar 

  14. Y. Ke, An efficient algorithm for link distance problems,Proc. 5th Annual ACM Symposium on Computational Geometry, 1989, pp. 69–78.

  15. D. T. Lee, Visibility of a simple polygon,Comput. Vision Graphics Image Process. 22 (1983), 207–221.

    Article  MATH  Google Scholar 

  16. W. Lenhart, R. Pollack, J. Sack, M. Sharir, R. Seidel, S. Suri, G. Toussaint, S. Whitesides, and C. Yap, Computing the link center of a simple polygon,Discrete Comput. Geom. 3 (1988), 281–293.

    Article  MATH  MathSciNet  Google Scholar 

  17. J. S. B. Mitchell, G. Rote, and G. Woeginger, Minimum-link paths among obstacles in the plane (extended abstract),Proc. 6th Annual ACM Symposium on Computational Geometry, 1990, pp. 63–72.

  18. J. S. B. Mitchell and E. Welzl, Dynamically maintaining a visibility graph under insertions of new obstacles, Manuscript, Cornell University, 1989.

  19. S. Suri, A linear time algorithm for minimum link paths inside a simple polygon,Comput. Vision Graphics Image Process.35 (1986), 99–110.

    Article  Google Scholar 

  20. S. Suri and J. O'Rourke, Worst-case optimal algorithms for constructing visibility polygons with holes,Proc. 2nd Annual Symposium on Computational Geometry, 1986, pp. 14–23.

Download references

Author information

Authors and Affiliations

  1. Applied Math, SUNY, 11794, Stony Brook, NY, USA

    Joseph S. B. Mitchell

  2. Institut für Mathematik, Technische Universität Graz, Kopernikusgasse 24, A-8010, Graz, Austria

    Günter Rote & Gerhard Woeginger

Authors
  1. Joseph S. B. Mitchell
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Günter Rote
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Gerhard Woeginger
    View author publications

    You can also search for this author inPubMed Google Scholar

Additional information

Communicated by Mikhail J. Atallah.

Joseph Mitchell was partially supported by NSF Grants IRI-8710858 and ECSE-8857642, and by a grant from Hughes Research Laboratories. This work was begun while Günter Rote and Gerhard Woeginger were at the Freie Universität Berlin, Fachbereich Mathematik, Institut für Informatik, and it was partially supported by the ESPRIT II Basic Research Actions Program of the EC under Contract No. 3075 (project ALCOM). Gerhard Woeginger acknowledges the support by the Fonds zur Förderung der Wissenschaftlichen Forschung, Projekt S32/01.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Mitchell, J.S.B., Rote, G. & Woeginger, G. Minimum-link paths among obstacles in the plane. Algorithmica 8, 431–459 (1992). https://doi.org/10.1007/BF01758855

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF01758855

Key words