Abstract
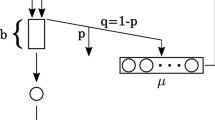
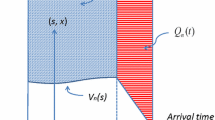
This paper studies approximations to describe the performance of a rate-control throttle based on a token bank, which is closely related to the standard G/G/1/C queue and the two-node cyclic network of ·/G/1/∞ queues. Several different approximations for the throttle are considered, but most attention is given to a Brownian or diffusion approximation. The Brownian approximation is supported by a heavy-traffic limit theorem (as the traffic intensity approaches the upper limit for stability) for which an upper bound on the rate of convergence is established. Means and squared coefficients of variation associated with renewal-process approximations for the overflow processes are also obtained from the Brownian approximation. The accuracy of the Brownian approximation is investigated by making numerical comparisons with exact values. The relatively simple Brownian approximation for the job overflow rate is not very accurate for small overflow rates, but it nevertheless provides important insights into the way the throttle design parameters should depend on the arrival-process characteristics in order to achieve a specified overflow rate. This simple approximation also provides estimates of the sensitivity of the overflow rates to the model parameters.
Similar content being viewed by others
References
Abate, J., and Whitt, W., 1988. Transient behavior of the M/M/1 queue via Laplace transforms.Adv. Appl. Prob., 20:145–178.
Anick, D., Mitra, D., and Sondhi, M.M., 1982. Stochastic theory of a data-handling system with multiple sources.Bell System Tech. J., 61:1871–1894.
Berger, A.W., 1991a. Overload control using a rate control throttle: Selecting token bank capacity for robustness to arrival rates.IEEE Trans. Aut. Cont., 36: 216–219. (AlsoProc. 28th IEEE Conf. on Decision and Control, 1989, 2527–2529).
Berger, A.W., 1991b. Performance analysis of a rate-control throttle where tokens and jobs queue.IEEE J. Sel. Areas Commun., 9:165–170. (alsoIEEE INFOCOMM, June 1990, 30–38).
Berger, A.W., and Whitt, W., 1990. A multi-class input-regulation throttle.Proc. 29th IEEE Conf. on Decision and Control, 2106–2111.
Berger, A.W., and Whitt, W., 1992. A multi-class rate-control throttle. In preparation.
Billingsley, P., 1968.Convergence of Probability Measures. New York: Wiley.
Borovkov, A.A., 1965. Some limit theorems in the theory of mass service. II.Theor. Prob. Appl., 10:375–400.
Borovkov, A.A., 1976.Stochastic Processes in Queueing Theory. New York: Springer-Verlag.
Budka, K.C., 1990. First- and Second-Order Stochastic Properties of Rate-Based Flow Control Mechanisms. Department of Industrial Engineering and Operations Research, Columbia University.
Budka, K.C., and Yao, D.D., 1990. Monotonicity and Convexity Properties of Rate Control Throttles. Department of Industrial Engineering and Operations Research, Columbia University.
Chen, H., and Mandelbaum, A., 1991a. Leontief systems, RBV's and RBM's.Proc. Imperial College Workshop on Applied Stochastic Processes. M. H. A. Davis and R. J. Elliott (eds), New York: Gordon and Breach.
Chen, H., and Mandelbaum, A., 1991b. Stochastic discrete flow networks: Diffusion approximations and bottlenecks.Ann Probab., 19: 1463–1519.
Chen, H., and Whitt, W., 1991. Diffusion approximations for open queueing networks with service interruptions. AT&T Bell Laboratories, Murray Hill, NJ.
Coffman, E.G., Jr., Puhalsky, A.A., and Reiman, M.I., 1991. Storage-limited queues in heavy traffic.Prob. Engr. Inf. Sci., 5: 499–522.
Coffman, E.G., Jr., and Reiman, M.I., 1984. Diffusion approximation for computer communications systems. pp. 33–53 inMathematical Computer Performance and Reliability; Iazcolla, G., Courtois, P.J. and Hordijk, A. (eds). Amsterdam: The North-Holland.
Cox, D.R., and Lewis, P.A.W., 1966.The Statistical Analysis of Series of Events. London: Metheun.
Csörgo″, M., Horváth, L., and Steinebach, J., 1987. Invariance principles for renewal processes.Ann. Probab, 15:1441–1460.
Dai, J.G., and Harrison, J.M., 1991. Steady-state analysis of RBM in a rectangle: Numerical methods and a queueing application.Ann. Appl. Prob., 1:16–35.
Doshi, B.T., and Heffes, H., 1983. Analysis of overload control schemes for a class of distributed switching machines.10th Int. Teletraffic Congress, Montreal, Canada, Paper No. 5.2.2.
Dupuis, P., and Ishii, H., 1991. On when the solution to the Skorokhod problem is Lipschitz continuous with applications.Stochastics, 35:31–62.
Eckberg, A.E., Luan, D.T., and Lucantoni, D.M., 1989. Bandwidth management: A congestion control strategy for broadband packet networks characterizing the throughput-burstiness filter.Int., Teletraffic Congress Specialist Seminar, Adelaide, Australia, (Sept.), Paper No. 4.4.
Eisenberg, M., 1983. A strict priority queueing system with overload control.10th Int. Teletraffic Congress, Montreal, Paper No. 1.3.2.
Elwalid, A., and Mitra, D., 1991. Analysis and design of rate-based congestion control of high-speed networks. I: Stochastic fluid models, access regulation.Queueing Systems, 9: 29–64.
Fendick, K.W., and Rodrigues, M., 1991. A heavy-traffic comparison of shared and segregated buffer schemes for queues with the head-of-line processor-sharing discipline.Queueing Systems, 9: 163–190.
Fendick, K.W., and Whitt, W., 1989. Measurements and approximations to describe the offered traffic and predict the average workload in a single-server queue.Proc. IEEE, 77:171–194.
Gaver, D.P., and Shedler, G.S., 1973a. Processor utilization in multiprogramming systems via diffusion approximations.Oper. Res., 21:569–576.
Gaver, D.P., and Shedler, G.S., 1973b. Approximate models for processor utilization in multiprogrammed computer systems.SIAM J. Comput., 2:183–192.
Gelenbe, E., 1975. On approximate computer system models.J. ACM., 22: 261–269.
Gelenbe, E., and Mitrani, I., 1980.Analysis and Synthesis of Computer Systems. New York: Academic Press.
Glynn, P.W., and Whitt, W., 1987. Sufficient conditions for functional-limit-theorem versions ofL=λW.Queueing Systems, 1:279–287.
Harrison, J.M., 1985.Brownian Motion and Stochastic Flow Systems. New York: Wiley
Heyman, D.P., and Stidham, S., Jr., 1980. The relation between customer and time averages in queues.Oper. Res., 28:983–994.
Iglehart, D.L., and Whitt, W., 1970a. Multiple channel queues in heavy traffic. IAdv. Appl. Prob., 2:150–177.
Iglehart, D.L., and Whitt, W., 1970b. Multiple channel queues in heavy traffic. II: Sequences, networks and batches.Adv. Appl. Prob., 2:355–369.
Kalashnikov, V.V., and Rachev, S.T., 1990.Mathematical Methods for Construction of Queueing Models. Belmont, CA.: Wadsworth and Brooks/Cole.
Keilson, J., 1979.Markov Chain Models—Rarity and Exponentiality. New York: Springer-Verlag.
Kemeny, J.G., and Snell, J.L., 1959. Finite Markov Chains. Princeton: Van Nostrand.
Kennedy, D.P., 1973. Limit theorems for finite dams.Stoch. Proc. Appl. 1:269–278.
Kimura, T., 1985. Refining diffusion approximations for GI/G/1 queues: A tight discretization method.Teletraffic Issues in an Advanced Information Society, ITC-11. M. Akiyama (ed.), Amsterdam: Elsevier, 317–323.
Kimura, T., Ohno, K., and Mine, H., 1979. Diffusion approximation for the GI/G/1 queueing systems with finite capacity. II: The stationary behavior.J. Oper. Res. Soc. Japan, 22:301–319.
Klincewicz, J.G., and Whitt, W., 1984. On approximations for queues. II: Shape constraints.AT&T Bell Lab. Tech. J., 63:139–161.
Kraemer, W., and Langenbach-Belz, M., 1976. Approximate formulae for the delay in the queueing system GI/G/1.Proc. Eighth Int. Teletraffic Cong., Melbourne, 235-1/8.
Kroner, H., Theimer, T.H., and Briem, U., 1990. Queueing models for ATM systems—A comparison.7th Teletraffic Congress Seminar Broadband Technologies, (Oct.), Morristown, NJ.
Kühn, P., 1976.Tables on Delay Systems. Institute of Switching and Data Technics, University of Stuttgart.
Neuts, M.F., 1986.Matrix-Geometric Solutions in Stochastic Models: An Algorithmic Approach. Baltimore: Johns Hopkins University Press.
Newell, G.F., 1982.Applications of Queueing Theory, 2nd ed., London: Chapman and Hall.
Rathgeb, E.P., 1990. Policing mechanisms for ATM networks—Modelling Performance comparison.7th Int. Teletraffic Congress Seminar, Broadband Technologies. (Oct.), Morristown, NJ.
Reiman, M.I., 1984. Open queueing networks in heavy traffic.Math. Oper. Res., 9:441–458.
Ross, S., 1982.Stochastic Processes. New York: Wiley.
Seelen, L.P., Tijms, H.C., and van Hoorn, M.H., 1985.Tables for Multi-Server Queues. Amsterdam: North-Holland.
Sidi, M., Liu, W.Z., Cidon, I., and Gopal, I., 1989. Congestion control through input rate regulation.GLOBECOM '89, (Nov.) 1764–1768, Dallas, TX.
Sohraby, K., and Sidi, M., 1990. On the performance of bursty and correlated sources subject to leaky bucket rate-based access control schemes.IEEE INFOCOM '91, (April), Bal Harbour, Florida, 426–434.
Sriram, K., and Whitt, W. 1986. Characterizing superposition arrival processes in packet multiplexers for voice and data.IEEE J. Sel. Areas Commun., SAC4:833–846.
Sweet, A.L., and Hardin, J.C., 1970. Solutions for some diffusion processes with two barriers.J. Appl. Prob., 7:423–431.
Turner, J. 1986. New directions in communications (or which way to the information age?).IEEE Comm. Mag., 24:8–15.
Whitt, W., 1969.Weak Convergence Theorems for Queues in Heavy Traffic. Ph.D. thesis, Cornell University.
Whitt, W., 1974. Preservation of rates of convergence under mapping.Z. Wahrsch. Gebiete, 29:39–44.
Whitt, W., 1980. Some useful functions for functional limit theorems.Math. Oper. Res., 5:67–85.
Whitt, W., 1982a. Approximating a point process by a renewal process. I: Two basic methods.Oper. Res., 30:125–147.
Whitt, W., 1982b. Refining diffusion approximations for queues.Oper. Res. Lett., 1:165–169.
Whitt, W., 1983. The queueing network analyzer.Bell System Tech. J., 62:2779–2815.
Whitt, W., 1984a. On approximations for queues. I: Extremal distributions.AT&T Bell Lab. Tech. J., 63:115–138.
Whitt, W., 1984b. On approximations for queues. III: Mixtures of exponential distributions.AT&T Bell Lab. Tech. J., 63:163–175.
Whitt, W., 1985. Approximation for the GI/G/m queues. AT&T Bell Laboratories.
Whitt, W., 1989. An interpolation approximation for the mean workload in a GI/G/1 queue.Oper. Res., 37:936–952.
Williams, R.J., 1991. Asymptotic variance parameters for the boundary local times of reflected brownian motion on a compact interval. Department of Mathematics, University of California at San Diego. To appear inJ. Appl. Prob.
Wolff, R.W., 1982. Poisson arrival see time averages.Oper. Res., 30:223–231.
Yao, D.D., and Buzacott, J.A., 1985a. Queueing models for a flexible machining station. Part I. Diffusion approximations.Eur. J. Oper. Res., 19:233–241.
Yao, D.D., and Buzacott, J.A., 1985b. Queueing models for a flexible machining station. Part II: The method of Coxian phases.Eur. J. Oper. Res., 19:242–252.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Berger, A.W., Whitt, W. The Brownian approximation for rate-control throttles and the G/G/1/C queue. Discrete Event Dyn Syst 2, 7–60 (1992). https://doi.org/10.1007/BF01797279
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF01797279
Key Words
- rate-control throttle
- token bank
- leaky bucket
- communication networks
- broadband integrated services digital networks (B-ISDNs)
- asynchronous transfer mode (ATM)
- G/G/1/C queues
- queues with finite waiting rooms
- overflow processes
- Brownian models
- diffusion approximations
- heavy traffic
- parametric-decomposition approximations