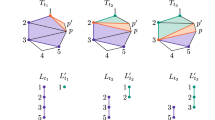
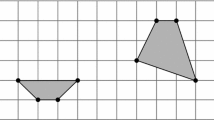
Abstract
We present the first quadratic-time algorithm for the greedy triangulation of a finite planar point set, and the first linear-time algorithm for the greedy triangulation of a convex polygon.
Similar content being viewed by others
References
A. Aggarwal,Research topics in computational geometry, Bulletin of EATCS 39 (October 1989), pp. 388–408.
A. Aggarwal, L. Guibas, J. Saxe and P. Shor,A linear time algorithm for computing the Voronoi diagram of a convex polygon, in Proc. of the 19th ACM Symposium on Theory of Computing, New York, pp. 39–45, 1987.
L. P. Chew,Constrained Delaunay triangulations, in: Proc. of the 3rd ACM Symposium on Computational Geometry, Waterloo, pp. 215–222, 1987.
P. D. Gilbert,New Results in Planar Triangulations, M.S. Thesis, Coordinated Science Laboratory, University of Illinois, Urbana, Illinois, 1979.
H. Edelsbrunner,Algorithms in Combinatorial Geometry, Texts and Monographs in Computer Science, Springer Verlag, Berlin, 1987.
S. A. Goldman,A space efficient greedy triangulation algorithm, Information Processing Letters 31 (1989) pp. 191–196.
C. Levcopoulos,An Θ(√n) lower bound for non-optimality of the greedy triangulation, Information Processing Letters 25 (1987), pp. 247–251.
D. T. Lee and A. Lin,Generalized Delaunay Triangulation for Planar Graphs, Discrete and Computational Geometry 1 (1986), Springer Verlag, pp. 201–217.
C. Levcopoulos and A. Lingas,On approximation behavior of the greedy triangulation for convex polygons, Algorithmica (1987) 2, pp. 175–193.
C. Levcopoulos, A. Lingas and J. Sack,Heuristics for optimum binary search trees and minimum weight triangulation problems, Theoretical Computer Science 66 (1989), pp. 181–203.
A. Lingas,A space efficient algorithm for the greedy triangulation, in: M. Thoma and A. Wyner, eds., Proc. 13th IFIP Conf. on System Modelling and Optimization, Tokyo (August 1987), Lecture Notes in Control and Information Sciences, Vol. 113 (Springer, Berlin, 1987), pp. 359–364.
A. Lingas,Greedy triangulation can be efficiently implemented in the average case, in: J. van Leeuwen, ed., Proc. International Workshop WG'88, Amsterdam (June 1988), Lecture Notes in Computer Science, Vol. 344 (Springer, Berlin, 1988), pp. 253–261.
A. Lingas,Voronoi diagrams with barriers and their applications, Information Processing Letters 32 (1989), pp. 191–198.
E. L. Lloyd,On triangulations of a set of points in the plane, Proc. of the 18th Annual IEEE Conference on the Foundations of Computer Science, Providence, 1977.
G. Manacher and A. Zorbrist,Neither the greedy nor the Delaunay triangulation of a planar point set approximates the optimal triangulation, Information Processing Letters 9 (1979).
F. P. Preparata and M. I. Shamos,Computational Geometry, An Introduction, Texts and Monographs in Computer Science, Springer Verlag, New York, 1985.
C. Wang and L. Schubert,An optimal algorithm for constructing the Delaunay triangulation of a set of line segments, in: Proc of the 3rd ACM Symposium on Computational Geometry, Waterloo, pp. 223–232, 1987.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Levcopoulos, C., Lingas, A. Fast algorithms for greedy triangulation. BIT 32, 280–296 (1992). https://doi.org/10.1007/BF01994882
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF01994882