Skip to main content
SpringerLink
Log in

The multilevel principle applied to sorting

  • Part I Computer Science
  • Published:
BIT Aims and scope Submit manuscript

Abstract

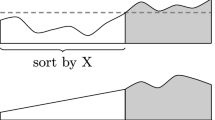
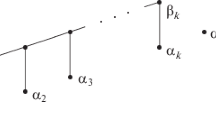
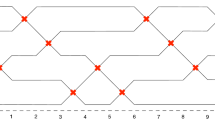
Sorting algorithms are developed in the setting of iterative multilevel methods. These algorithms borrow aggregation techniques from algorithms used for the numerical solution of elliptic partial differential equations which are of optimal order in running time and storage space for structured problems. A computationally inexpensive preconditioner drives random data chosen from known distributions towards a special case for which the new sorting algorithms are of optimal order.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. A. Aho, J. Hopcroft, and J. Ullman,The Design and Analysis of Computer Algorithms, Addison-Wesley, Reading, MA, 1974.

    MATH  Google Scholar 

  2. D. C. S. Allison and M. T. Noga,Usort: an efficient hybrid of distributive partitioning sorting, BIT, 22 (1982), pp. 135–139.

    Article  MATH  MathSciNet  Google Scholar 

  3. R. E. Bank and C. C. Douglas,Sharp estimates for multigrid rates of convergence with general smoothing and accleration, SIAM J. Numer. Anal., 22 (1985), pp. 617–633.

    Article  MATH  MathSciNet  Google Scholar 

  4. A. Brandt,Multi-level adaptive solution to boundary-value problems, Math. Comp., 31 (1977), pp. 333–390.

    Article  MATH  MathSciNet  Google Scholar 

  5. F. Chatelin and W. L. Miranker,Acceleration by aggregation of successive approximation methods, Lin. Alg. Appl., 43 (1982), pp. 17–47.

    Article  MATH  MathSciNet  Google Scholar 

  6. W. Dobosiewicz,An efficient variation of bubble sort, Info. Proc. Lett., 11 (1980), pp. 5–6.

    Article  Google Scholar 

  7. W. Dobosiewicz,Sorting by distributive partitioning, Info. Lett., 7 (1978), pp. 1–6.

    Article  MATH  MathSciNet  Google Scholar 

  8. C. C. Douglas,Multigrid algorithms for elliptic boundary-value problems, PhD thesis, Yale University, May 1982. Also, Computer Science Department, Yale University, Technical Report 223.

  9. C. C. Douglas,Multi-grid algorithms with applications to elliptic boundary-value problems, SIAM J. Numer. Anal., 21 (1984), pp. 236–254.

    Article  MATH  MathSciNet  Google Scholar 

  10. C. C. Douglas and W. L. Miranker,Multilevel sorting algorithms, Tech. Report 14736, IBM Research Division, Yorktown Heights, New York, 1989.

    Google Scholar 

  11. P. J. Janus and E. A. Lamagna,An adaptive method for unknown distributions in distributive partitioned sorting, IEEE Trans. on Computers, 34 (1985), pp. 367–372.

    Article  MATH  Google Scholar 

  12. J. S. Kowalik and Y. B. Yoo,Implementing a distributive sort program, J. Inform. Optimaliz. Sci., 2 (1981), pp. 28–33.

    MathSciNet  Google Scholar 

  13. H. Meijer and S. G. Akl,The design and analysis of a new hybrid sorting algorithm, Inf. Proc. Lett., 10 (1980), pp. 213–218.

    Article  MATH  MathSciNet  Google Scholar 

  14. W. L. Miranker and V. Y. Pan,Methods of aggregation, Lin. Alg. Appl. 29 (1980), pp. 231–257.

    Article  MATH  MathSciNet  Google Scholar 

  15. M. van der Nat,A fast sortin algorithm, a hybrid of distributive and merge sorting, Inf. Proc. Lett., 10 (1980), pp. 163–167.

    Article  Google Scholar 

  16. M. T. Noga and D. C. S. Allison,Sorting in linear expected time, BIT, 25 (1985), pp. 451–465.

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Mathematical Sciences Department, IBM Research Division, Thomas J. Watson Research Center, P. O. Box 218, 10598, Yorktown Heights, New York, USA

    Craig C. Douglas & Willard L. Miranker

Authors
  1. Craig C. Douglas
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Willard L. Miranker
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Douglas, C.C., Miranker, W.L. The multilevel principle applied to sorting. BIT 30, 177–195 (1990). https://doi.org/10.1007/BF02017340

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02017340

AMS(MOS) subject classifications

Search

Navigation