Skip to main content
Springer Nature Link
Log in

Pollution control: A differential game approach

  • Published:
Annals of Operations Research Aims and scope Submit manuscript

Abstract

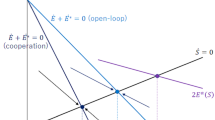
Transnational pollution is formulated as a differential game between two sovereign governments. The symmetric open loop Nash equilibrium is shown to yield more pollution than in a cooperative solution. A model of Stackelberg leadership in pollution control is also investigated. The possibility of limit cycles is illustrated, using bifurcation theory.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. T. Basar and B.J. Olsder,Dynamic Non-Cooperative Game Theory (Academic Press, 1982).

  2. W.A. Brock and J. Sheinkman, The global asymptotic stability of optimal control with applications to dynamic economic theory, in:Applications of Control Theory to Economic Analysis, ed. J.D. Pitchford and S.J. Turnovsky (North-Holland, Amsterdam, 1977).

    Google Scholar 

  3. J.M. Conrad and L.J. Olson, Polluted control and resource management, Working Paper, Department of Agricultural Economics, Cornell University, New York (1990).

    Google Scholar 

  4. E. Dockner, Local stability analysis in optimal control problems with two state variables, in:Optimal Control Theory and Economic Analysis 2, ed. G. Feichtinger (North-Holland, Amsterdam, 1985).

    Google Scholar 

  5. C. Fershtman and M. Kamien, Dynamic duopolistic competition with sticky prices, Econometrica 55(1987)257.

    Google Scholar 

  6. B.A. Forster, Optimal consumption planning in a polluted environment, Econ. Record 49(1973)534.

    Google Scholar 

  7. B.A. Forster, Optimal pollution control with a non-constant exponential rate of decay, J. Environ. Econ. Manag. 2(1975)1.

    Google Scholar 

  8. J. Guckenheimer and P. Holmes,Non-Linear Oscillations, Dynamical Systems, and Bifurcation of Vector Fields (Springer, 1983).

  9. M.C. Kemp, N.V. Long and K. Shimomura, Cyclical and non-cyclical redistributive taxation, Working Paper, Department of Economics, University of New South Wales, Australia (1990).

    Google Scholar 

  10. C.G. Plourde, A model of waste accumulation and disposal, Can. J. Econ. 5(1972)115.

    Google Scholar 

  11. C.G. Plourde and D. Yeung, A model of industrial pollution in a stochastic environment, J. Environ. Econ. Manag. 17(1989)100.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Economics, McGill University, 855 Sherbrooke Street West, H3A 2T7, Montreal, Quebec, Canada

    N. V. Long

Authors
  1. N. V. Long
    View author publications

    You can also search for this author inPubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Long, N.V. Pollution control: A differential game approach. Ann Oper Res 37, 283–296 (1992). https://doi.org/10.1007/BF02071061

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02071061

Keywords