Abstract
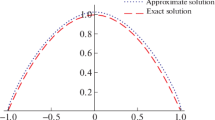
We consider the non-linear boundary value problem with small perturbation parameter ε. We find its numerical solution by using Richardson extrapolation on a special non-uniform discretization mesh. Both, high accuracy and uniformity in ε, are obtained. Numerical examples are provided.
Zusammenfassung
Wir betrachten die nichtlineare Randwertaufgabe mit kleinem Störungsparameter ε. Wir finden ihre numerische Lösung unter Anwendung von Richardson-Extrapolation mit einem speziellen nichtäquidistanten Diskretisierungsgitter. Man erhält gleichzeitig große Genauigkeit und gleichmäßige Konvergenz. Numerische Beispiele werden angegeben.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Bakhvalov, N. S.: K optimizacii metodov resheniya kraevyh zadach pri nalichii pogranichnogo sloya. Zh. vychisl. mat. i mat. fiz.9, 841–859 (1969).
Bohl, E.: Finite Modelle gewöhnlicher Randwertaufgaben. Stuttgart: B. G. Teubner 1981.
Bohl, E., Lorenz, J.: Inverse monotonicity and difference schemes of higher order. A summary for two-point boundary value problems. Aeq. Math.19, 1–36 (1979).
Doolan, E. P., Miller, J. J. H., Schilders, W. H. A.: Uniform Numerical Methods for Problems with Initial and Boundary Layers. Dublin: Boole Press 1980.
Henrici, P.: Discrete Variable Methods in Ordinary Differential Equations. New York: Wiley 1962.
Herceg, D.: A uniformly convergent scheme with quasi-constant fitting factors. Zb. rad. Prir.-Mat. Fak. Univ. Novom Sadu Ser. Mat.11, 105–115 (1981).
Herceg, D., Vulanović, R.: Some finite-difference schemes for a singular perturbation problem on a non-uniform mesh. Zb. rad. Prir.-Mat. Fak. Univ. Novom Sadu, Ser. mat.11, 117–134 (1981).
Keller, H. B.: Accurate difference methods for nonlinear two-point boundary value problems. SIAM J. Numer. Anal.11, 305–320 (1974).
Lorenz, J.: Stability and monotonicity properties of stiff quasilinear boundary problems. Zb. rad. Prir. Mat. Fak. Univ. Novom Sadu, Ser. mat.12, 151–176 (1982).
Marchuk, G. I., Shaidurov, V. V.: Povishenie tochnosti reshenii raznostnyh shem. Moskva: Nauka 1979.
Shishkin, G. T.: Raznostnaya shema na neravnomernoi setke dlya differencial'nogo uravneniya s malym parametrom pri starshei proizvodnoi. Zh. vychisl. mat. i mat. fiz.23, 609–619 (1983).
Vlanović, R.: An exponentially fitted scheme on a non-uniform mesh. Zb. rad. Prir.-Mat. Fak. Univ. Novom Sadu, Ser. mat.12, 205–215 (1982).
Vulanović, R.: On numerical solution of a type of singularly perturbed boundary value problem by using a special discretization mesh. Zb. rad. Prir.-Mat. Fak. Univ. Novom Sadu, Ser. mat.13, 187–201 (1983).
Weiss, R.: An analysis of the box and trapezoidal schemes for linear singularly perturbed boundary value problems. Math Comp.42, 41–67 (1984).
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Vulanović, R., Herceg, D. & Petrović, N. On the extrapolation for a singularly perturbed boundary value problem. Computing 36, 69–79 (1986). https://doi.org/10.1007/BF02238193
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF02238193