Abstract
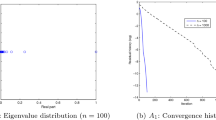
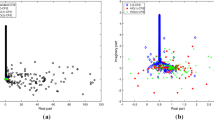
The discretization of linear integral equations for elliptic boundary value problems by the boundary element method yields linear systems of simultaneous equations with filled matrices. The structure of these matrices allows Fourier methods to be used to determine preconditioning matrices such that fast iterative solution of the linear system of algebraic equations is possible. The preconditioning method is applicable to Fredholm integral equations of the first kind with non-smooth convolutional principal part as well as to Fredholm integral equations of the second kind. Numerical examples are presented.
Zusammenfassung
Die Diskretisierung von linearen Integralgleichungen für elliptische Randwertaufgaben durch die Randelementmethode gibt lineare Gleichungssysteme mit gefüllten Matrizen. Die Struktur dieser Matrizen läßt Vorkonditionierung durch Fourier-Methoden zu, was schnelles iteratives Lösen des Gleichungssystems von algebraischen Gleichungen ermöglicht. Die Vorkonditionierungsmethode ist verwendbar für Fredholmsche Integralgleichungen erster Art mit unglattem Kern vom Faltungstyp, sowie für Fredholmsche Integralgleichungen zweiter Art. Numerische Beispiele werden präsentiert.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Arnold, N. A., Wendland, W. L.: On the asymptotic convergence of collocation methods. Math. Comp.41, 349–381 (1984).
Atkinson, K. E.: A survey of numerical methods for the solution of Fredholm integral equations of the 2nd kind. Philadelphia: SIAM 1976.
de Boor, C.: A practical guide to splines. New York: Springer 1978.
Henrici, P.: Fast Fourier methods in computational complex analysis. SIAM Rev.21, 481–527 (1979).
Hemker, P. W., Schippers, H.: Multiple grid methods for the solution of Fredholm integral equations of the second kind. Math. Comp.36, 215–232 (1981).
Hoidn, H.-P.: Die Kollokationsmethode angewandt auf die Symmsche Integralgleichung. Thesis, Swiss Institute of Technology, Zürich (1983).
Hsiao, G. C., Kopp, P., Wendland, W. L.: A Galerkin collocation method for some integral equations of the first kind. Computing25, 89–130 (1980).
Hsiao, G. C., Kopp, P., Wendland, W. L.: Some applications of a Galerkin-collocation method for boundary integral equations of the first kind. Fachbereich Mathematik, Technische Hochschule Darmstadt, Preprint 768 (1983).
Lanczos, C.: Discourse on Fourier series. London: Oliver & Boyd 1966.
Reichel, L.: On the determination of collocation points for solving some problems for the Laplace opeator. J. Comput. Appl. Math.11, 175–196 (1984).
Reichel, L.: A fast method for solving certain integral equations of the first kind with application to conformal mapping. J. Comput. Appl. Math., to appear.
Wendland, W. L.: On Galerkin-collocation methods for integral equations of elliptic boundary value problems. In: Numerical treatment of integral equations (Albrecht, J., Collatz, L., eds.) pp. 244–275. Basel: Birkhäuser 1980.
Wendland, W. L.: On the asymptotic convergence of some boundary element methods. In: MAFELAP 1981 (Whiteman, J., ed.) pp. 281–312. London: Academic Press 1982.
Wendland, W. L.: Elliptic systems in the plane. London: Pitman 1979.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Reichel, L. A method for preconditioning matrices arising from linear integral equations for elliptic boundary value problems. Computing 37, 125–136 (1986). https://doi.org/10.1007/BF02253186
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF02253186