Skip to main content
Springer Nature Link
Log in

PiecewiseC 1-shape-preserving Hermite interpolation

Stückweise gestalterhaltendeC 1-Hermite-Interpolation

  • Published:
Computing Aims and scope Submit manuscript

Abstract

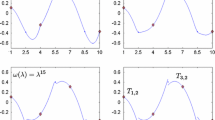
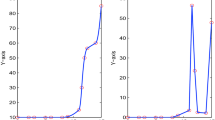
A local scheme for piecewiseC 1-Hermite interpolation is presented. The interpolant is obtained patching together cubic with quadratic polynomial segments; it is co-monotone and/or co-convex with the data. Under appropriate assumptions the method is fourth-order accurate.

Zusammenfassung

Ein lokaler Ansatz zur stückweisenC 1-Hermite-Interpolation wird vorgestellt. Die Interpolierende besteht aus zusammengesetzten kubischen und quadratischen Segmenten; sie erhält die Monotonie und/oder die Konvexität der Daten. Unter geeigneten Voraussetzungen approximier sie von vierter Ordnung.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Conti, C., Morandi, R.: A short note on admissible slopes forC 1 piecewise convex interpolation. Rapp. Int. Dip. Energetica (1994).

  2. Costantini P.: An algorithm for computing shape-preserving interpolating splines of arbitrary degree. J. Comput. Appl Math.22, 89–136 (1988).

    Article  Google Scholar 

  3. Edelman A., Micchelli C. A.: Admissible slopes for monotone and convex interpolation. Numer. Math.51, 441–458 (1987).

    Article  Google Scholar 

  4. Gasparo M. G., Morandi R.: Piecewise cubic monotone interpolation with assigned slopes. Computing46, 355–365 (1991).

    Google Scholar 

  5. Gregory G. A., Delbourgo R.: Piecewise rational quadratic interpolation to montonic data. I.M.A.J. Numer. Anal.2, 123–130 (1982).

    Google Scholar 

  6. Manni C.: Parametric comonotone hermite interpolation. Preprint (1994).

  7. Yan Z.: Piecewise cubic curve fitting algorithm. Math. Comp.49, 203–213 (1987).

    Google Scholar 

  8. Zhang Z., Yang Z., Zhang C.: Monotone piecewise curve fitting algorithms. J. Comp. Math.12, 165–174 (1994).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Dipartimento di Energetica, Università di Firenze, Via C. Lombroso 6/17, I-50134, Firenze, Italy

    C. Conti & R. Morandi

Authors
  1. C. Conti
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. R. Morandi
    View author publications

    You can also search for this author inPubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Conti, C., Morandi, R. PiecewiseC 1-shape-preserving Hermite interpolation. Computing 56, 323–341 (1996). https://doi.org/10.1007/BF02253459

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02253459

AMS Subject Classifications

Key words