Skip to main content
Springer Nature Link
Log in

The improved radial basis function neural network and its application

  • Original Article
  • Published:
Artificial Life and Robotics Aims and scope Submit manuscript

Abstract

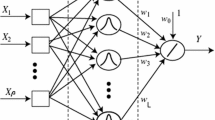
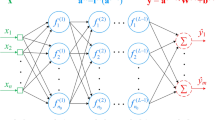
Compared with other feed-forward neural networks, radial basis function neural networks (RBFNN) have many advantages which make them more suitable for nonlinear system modeling, and they have recently received considerable attention. In this paper, a RBFNN is employed to model strongly nonlinear systems. First, the problems of nonlinear system modeling are analyzed, and then the structure of the RBFNN as well as the training algorithm are improved to solve these problems. Finally, an industrial high-purity distillation column, which is a strongly nonlinear system, is successfully modeled with the improved RBFNN. Owing to the complexities of a nonlinear system, it is necessary to use a real-time model correction method to modify the parameters of the RBFNN model in real time. One efficient method is proposed in this paper. The idea is to employ the Givens transformation to modify the parameters of the RBFNN-based model.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Chen S, Cowan CFN, Grant PM (1991) Orthogonal least squares learning algorithm for radial basis function networks. IEEE Trans. Neural Networks 2(2):302–309

    Article  Google Scholar 

  2. Chen S, Grant PM, Cowan CFN (1992) Orthogonal least squares algorithm for training multioutput radial basis function networks. IEE Proc-F 139(6):378–384

    Google Scholar 

  3. Moody J, Darken C (1989) Fast learning in networks of locally tuned processing units. Neural Comput 1:281–294

    Google Scholar 

  4. Bianchini M, Frasconi P, Gori M (1995) Learning without local minima in radial basis function networks. IEEE Trans. Neural Networks 3:749–755

    Article  Google Scholar 

  5. Girosi F, Poggio T (1990) Networks and the best approximation property. Biol Cybernetics 63:169–176

    Article  MATH  MathSciNet  Google Scholar 

  6. Kung SY (1993) Digital neural networks. PTR Prentice-Hall, Englewood Cliffs

    MATH  Google Scholar 

  7. Xu L, Krzyzak A, Oja E (1993) Rival, penalized competitive learning for clustering analysis, RBF net, and curve detection. IEEE Trans. Neural Networks 4(4):636–649

    Article  Google Scholar 

  8. Holcomb T, Morari M (1993) Local training for radial basis function networks: Towards solving the hidden unit problem. American Control Conference, 1993, pp. 2331–2335

  9. Chen S, Billings SA, Grant PM (1992) Recursive hybrid algorithm for nonlinear identification using radial basis function networks. Int J Control 55(5):1051–1070

    MATH  MathSciNet  Google Scholar 

  10. Wang X, Luo R, Shao H (1996) Designing a soft sensor for a distillation column with the fuzzy distributed radial basis function neural network. Proceedings of the 35th IEEE Conference on Decision and Control, Kobe, Japan, December 11–13, 1996, pp 1714–1719

  11. Wang X (1997) The radial basis function neural network and its applications to process control. PhD dissertation, Shanghai Jiao Tong University

  12. Gentleman WE (1973) Least squares computations by Givens transformations without squares roots. J Inst Math Appl 12:329–336

    MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Automation, Shanghai Jião Tong University, 200030, Shanghai, People's Republic of China

    Xudong Wang, Yuhua Ding & Huihe Shao

Authors
  1. Xudong Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Yuhua Ding
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Huihe Shao
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Xudong Wang.

About this article

Cite this article

Wang, X., Ding, Y. & Shao, H. The improved radial basis function neural network and its application. Artificial Life and Robotics 2, 8–11 (1998). https://doi.org/10.1007/BF02471145

Download citation

  • Received:

  • Accepted:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02471145

Key words