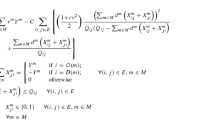Abstract
We model a server that allocates varying amounts of bandwidth to “customers” during service. Customers could be computer jobs with demands for storage bandwidth or they could be calls with demands for transmission bandwidth on a network link. Service times are constants, each normalized to 1 time unit, and the system operates in discrete time, with packing (scheduling) decisions made only at integer times. Demands for bandwidths are for fractions of the total available and are limited to the discrete set {1/k, 2/k, …, 1} wherek is a given parameter. More than one customer can be served at a time, but the total bandwidth allocated to the customers in service must be at most the total available. Customers arrive ink flows and join a queue. Thejth flow has rate λ j and contains just those customers with bandwidth demandsj/k.
We study the performance of the two packing algorithms First Fit and Best Fit, both allocating bandwidth by a greedy rule, the first scanning the queue in arrival order and the second scanning the queue in decreasing order of bandwidth demand. We determine necessary and sufficient conditions for stability of the system under the two packing rules. The average total bandwidth demand of the arrivals in a time slot must be less than 1 for stability under any packing rule, i.e., the condition
must hold. We prove that if the arrival rates λ1, …, λ k−1 are symmetric, i.e., λ i =λ k−i for alli, 1 ≤i ≤k − 1, theρ<1 is also sufficient for stability under both rules. Our Best Fit result strengthens an earlier result confined to Poisson flows and equal rates λ1=…=λ k − 1, and does so using a far simper proof. Our First Fit result is completely new. The work here extends earlier results on bandwidth packing in multimedia communication systems, on storage allocation in computer systems, and on message transmission along slotted communication channels.
It is not surprising thatρ<1 is sufficient under Best Fit, since in a congested system, Best Fit tends to serve two complementary (matched) customers in each time slot, with bandwidth demands beingi/k and (k − i)/k for somei, 1 ≤i ≤k − 1. It is not so obvious, however, thatρ<1 is also sufficient under First Fit. Interestingly, when the system becomes congested, First Fit exhibits a “self-organizing” property whereby an ordering of the queue by time of arrival becomes approximately the same as an ordering by decreasing bandwidth demand.
Similar content being viewed by others
References
S. Albers and M. Mitzenmacher. Average-Case Analysis of First Fit and Random Fit Bin Packing.Proceedings of the Ninth Annual ACM-SIAM Symosium on Discrete Algorithms (1998), pp. 290–299.
H. Chen. Fluid Approximations and Stability of Multiclass Queueing Networks: Work-Conserving Disciplines.Annals of Applied Probability, Vol. 5 (1995), pp. 637–665.
E. G. Coffman, Jr., A. Feldmann, N. Kahale, and B. Poonen. Computing Call Admission Capacities in Linear Networks. Bell Labs, Lucent Technologies, Murray Hill, NJ 07974 (1997), submitted for publication.
E. G. Coffman, Jr., M. R. Garey, and D. S. Johnson. Approximation Algorithms for Bin Packing: A Survey. InApproximation Algorithms for NP-Complete Problems, D. S. Hochbaum (ed.). PWS, Boston, MA (1995), pp. 46–93.
E. G. Coffman, Jr., S. Halfin, A. Jean-Marie, and P. Robert. Stochastic Analysis of a Slotted, FIFO Communication Channel.IEEE Transactions on Information Theory, Vol. 39 (1993), pp. 1555–1566.
E. G. Coffman, Jr., D. S. Johnson, P. W. Shor, and R. R. Weber. Bin Packing with Discrete Item Sizes, Part II: Tight Bounds on First Fit.Random Structures and Algorithms, Vol. 10 (1997), pp. 69–101.
J. G. Dai. On the Positive Harris Recurrence for Open Multiclass Queueing Networks: A Unified Approach via Fluid Limit Models.Annals of Applied Probability, Vol. 5 (1995), pp. 49–77.
J. G. Dai and S. P. Meyn. Stability and Convergence of Moments for Open Multiclass Queueing Networks via Fluid Limit Models.IEEE Transactions on Automatic Control, Vol. 40 (1995), pp. 1889–1904.
C. Kipnis and P. Robert. A Dynamic Storage Process.Stochastic Processes and Their Applications, Vol. 34 (1990), pp. 155–169.
V. A. Malyshev and M. V. Menshikov. Ergodicity, Continuity, and Analyticity of Countable Markov Chains.Transactions of Moscow Mathematical Society, Vol. 39 (1979), pp. 3–48.
A. N. Rybko and A. L. Stolyar. Ergodicity of Stochastic Processes Describing the Operation of Open Queueing Networks.Problems of Information Transmission, Vol. 28 (1992), pp. 199–220.
A. L. Stolyar. On the Stability of Multiclass Queueing Networks: A Relaxed Sufficient Condition via Limiting Fluid Processes.Markov Processes and Related Fields, Vol. 1, No. 4 (1995), pp. 491–512.
Author information
Authors and Affiliations
Additional information
Communicated by H. Prodinger and W. Szpankowski.
Part of the work of this author was completed while he was with AT&T Labs-Research, Murray Hill, NJ 07974, USA (now located in Florham Park, NJ 07932, USA).
Online publication October 6, 2000.
Rights and permissions
About this article
Cite this article
Coffman, E.G., Stolyar, A.L. Bandwidth packing. Algorithmica 29, 70–88 (2001). https://doi.org/10.1007/BF02679614
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF02679614