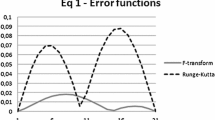
Abstract
For an inverse-monotone boundary value problem with the nonlinear ODE –ɛu" + sinh(u)=1,ɛ>0, u(0)=u(1)=0, applications of the following enclosure methods are presented and discussed:
-
(i)
on the basis of a piecewise replacement of sinh(u) by polynomials, the construction of monotone sequences of upper and lower bounds foru;
-
(ii)
on the basis of Lohner’s enclosure algorithms for solutions of ODEs, simple and multiple shooting methods.
Existence of a classical solution follows from literature and (independently) from the execution of (ii). Whereas (i) requires the inverse-monotonicity of the problem, this is not so for (ii). For small ε, the unique solution of the BVP is strongly repellent.
Similar content being viewed by others
References
Adams, E.: Periodic solutions: enclosure, verification, and applications. In: Computer arithmetic and self-validating numerical methods (Ulrich, Ch., ed.), pp. 199–245. Boston: Academic Press 1990.
Adams, E., Ansorge, R., Grossmann, C., Roos, H.-G. (eds.): Discretization in differential equations and enclosures. Berlin: Akademie Verlag 1987.
Adams, E., Holzmüller, A., Straub, D.: The periodic solutions of the Oregonator and verification of results. In: Scientific computation with automatic result verifications (Kulisch, U., Stetter, H.J, eds.), pp. 111–121. Wien New York: Springer 1988 (Computing Suppl. 6).
Adams, E., Spreuer, H.: Konvergente numerische Schrankenkonstruktionen mit Spline-Funktionen für nichtlineare gewöhnliche bzw. parabolische Randwertaufgaben. In: Interval mathematics (Nickel, K., ed.), pp. 118–126. Berlin Heidelberg, New York: Springer 1975.
Alefeld, G., Herzberger, J.: Introduction to interval computations. New York: Springer 1983.
Al-Zanaidi, M., Grossmann, C.: Monotone iteration discretization algorithm for BVP’s. Computing31, 59–74 (1989).
Ascher, U.: On numerical differential algebraic problems with applications to semiconductor device simulation. SIAM J. Numer. Anal.26, 517–538 (1989).
Ascher, U., Mattheij, R. M., Russel, R. D.: Numerical solution of boundary value problems for ordinary differential equations. Englewood Cliffs: Prentice Hall 1988.
Ascher, U., Weiss, R.: Collocation for singular perturbation problems III: Nonlinear problems without turning points. SIAM J. Sci. Statist. Comput.5, 811–829 (1984).
Baumann, K.: Einschließungsmethoden für zwei Klassen von Differentialgleichungen aus dem Ingenieurwesen. Diplomarbeit, Karlsruhe 1993.
DeBoor, C.: A practical guide to splines. Berlin Heidelberg New York: Springer 1978.
Eijgenraam, P.: The solution of initial value problems using interval arithmetic. Stichting Mathematisch Centrum Amsterdam, Mathematical Centre Tracts 144, 1981.
Grossmann, C.: Monotone discretization of two-point bounday value problems and related numerical methods. In: [2], pp. 99–122.
Grossmann, C., Krätzschmar, M., Roos, H.-G.: Gleichmäßig einschließende Diskretisierungsverfahren für schwach nichtlineare Randwertaufgaben. Numer. Math.49, 95–110 (1986).
Grossmann, C., Roos, H.-G.: Enclosing discretization for singular and singularly perturbed boundary value problems. In: Numerical methods in singularly perturbed problems, (Roos, H.G., et al., eds), pp. 71–82. TU Dresden 1991.
Hairer, E., Norsett, S. P., Wanner, G.: Solving ordinary differential equations I: Nonstiff problems. Berlin Heidelberg New York Tokyo: Springer 1987.
Hammer, R., et al.: Numerical toolbox for verified computing I, theory, algorithms and PASCAL-XSC programs. Berlin Heidelberg New York Tokyo: Springer 1991.
Hemker, P.W.: A numerical study of stiff two-point boundary value problems. Ph.D. Thesis, Amsterdam 1977.
Jordan, D. W., Smith, P.: Nonlinear ordinary differential equations. Oxford: Clarendon Press 1977.
Kadalbajoo, M. K., Bawa, R. K.: Cubic spline method for a class of nonlinear singularly-perturbed boundary-value problems. J. Optim. Theory Appl.76, 415–428 (1993).
Kinderlehrer, D., Stampacchia, G.: An introduction to variational inequalities and their applications. New York: Academic Press 1980.
Klatte, R., et al.: PASCAL-XSC Sprachbeschreibung mit Beispielen. Berlin Heidelberg New York: Tokyo Springer 1991; [English translation: Springer, 1992].
Krätzschmar, M.: Iterationsverfahren zur Lösung schwach nichtlinearer elliptischer Randwertaufgaben mit monotoner Lösungseinschließung. Ph.D. Thesis, Dresden 1983.
Kulisch, U., Miranker, W. L.: Computer arithmetic in theory and practice. New York: Academic Press 1981.
Lohner, R.: Einschließung der Lösung gewöhnlicher Anfangs- und Randwertaufgaben und Anwendungen. Diss., Univ. Karlsruhe, 1988.
Lohner, R. et al.: Numerical toolbox for verified computing II/III, theory, algorithms and PASCAL-XSC programs. Heidelberg New York Tokyo: Springer 1990.
O’Malley, R. E.: Singular perturbation methods for ordinary differential equations. Applied Mathematical Sciences, vol. 89. New York: Springer 1991.
Plum, M.: Computer-aided existence proofs for two-point boundary value problems. Computing46, 19–34 (1991).
Roos, H. G., Stynes, M., Tobiska, L.: Numerical methods for singularly perturbed differential equations. Berlin Heidelberg New York Tokyo: Springer 1996.
Schröder, J.: Operator inequalities. New York: Academic Press 1980.
Schröder, J.: Operator inequalities and applications. In: Inequalities (Norrie, E.W., ed.), pp. 163–210. New York: Marcel Dekker 1991.
Selberherr, S.: Analysis and simulation of semiconductor devices. Heidelberg New York: Springer 1984.
Sprekels, J., Voss, H.: Pointwise inclusions of fixed points by finite dimensional iteration schemes. Numer. Math.32, 381–392 (1979).
Spreuer, H.: A method for the computation of bounds with convergence of arbitrary order for ordinary linear boundary value problems. JMAA81, 99–133 (1981).
Stoer, J., Bulirsch, R.: Einführung in die numerische Mathematik, II. Berlin Heidelberg New York: Springer 1973.
Walter, W.: Differential and integral inequalities. Berlin Heidelberg New York: Springer 1970.
Author information
Authors and Affiliations
Additional information
Dedicated to Professor William F. Ames on the occasion of his 70th birthday
Supported by grant SM 093 of Kuwait University
Rights and permissions
About this article
Cite this article
Adams, E., Baumann, K. & Grossmann, C. Comparison of direct to shooting enclosures for an inverse-monotone boundary value problem with locally steep solution. Computing 59, 63–83 (1997). https://doi.org/10.1007/BF02684404
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF02684404