Skip to main content
Springer Nature Link
Log in

Bayesian and non-bayesian analysis of gamma stochastic frontier models by Markov Chain Monte Carlo methods

  • Published:
Computational Statistics Aims and scope Submit manuscript

Summary

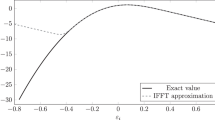
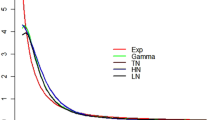
This paper considers simulation-based approaches for the gamma stochastic frontier model. Efficient Markov chain Monte Carlo methods are proposed for sampling the posterior distribution of the parameters. Maximum likelihood estimation is also discussed based on the stochastic approximation algorithm. The methods are applied to a data set of the U.S. electric utility industry.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Figure 1
Figure 2

Similar content being viewed by others

References

  • Aigner, D., Lovell, C. A. K. & Schmidt, P. (1977). “Formulation and estimation of stochastic frontier production function models,”Journal of Econometrics, 6, 21–37.

    Article  MathSciNet  Google Scholar 

  • Beckers, D. & Hammond, C. (1987). “A tractable likelihood function for the normal-gamma stochastic frontier model,”Economics Letters, 24, 33–38.

    Article  MathSciNet  Google Scholar 

  • Besag, J. & Green, P. (1993). “Spatial statistics and Bayesian computation,”Journal of the Royal Statistics Society, B55, 25–37.

    MathSciNet  MATH  Google Scholar 

  • Booth, J. G. & Hobert, J. P. (1999). “Maximizing generalized linear mixed model likelihoods with an automated Monte Carlo EM algorithm,”Journal of the Royal Statistics Society, B61, 265–285.

    Article  Google Scholar 

  • van den Broeck, J., Koop, G., Osiewalski, J. & Steel, M. F. J. (1994). “Stochastic frontier models,”Journal of Econometrics, 61, 273–303.

    Article  Google Scholar 

  • Charnes, A., Cooper, W. W. & Rhodes, E. (1978). “Measuring the efficiency of decision-making units,”European Journal of Operational Research, 2, 429–444.

    Article  MathSciNet  Google Scholar 

  • Chib, S. (1995). “Marginal likelihood from the Gibbs output,”Journal of the American Statistical Association, 90, 1313–1321.

    Article  MathSciNet  Google Scholar 

  • Chib, S. (2001). “Markov chain Monte Carlo methods: Computation and inference,” inHandbook of Econometrics, Vol. 5 (eds J. Heckman and E. Learner), North Holland, Amsterdam, 3569–3649.

    Chapter  Google Scholar 

  • Chib, S. & Greenberg, E. (1995). “Understanding the Metropolis-Hastings algorithm,”American Statistician, 49, 327–335.

    Google Scholar 

  • Chib, S. & Jeliazkov, I. (2001). “Marginal likelihood from the Metropolis-Hastings output,”Journal of the American Statistical Association, 96, 270–281.

    Article  MathSciNet  Google Scholar 

  • Chib, S. & Jeliazkov, I. (2002). “Accept-reject Metropolis-Hastings sampling and marginal likelihood estimation,” Technical Report, Washington University.

  • Christensen, L. R. & Greene, W. H. (1976). “Economies of scale in U.S. electric power generation,”Journal of Political Economy, 84, 655–676.

    Article  Google Scholar 

  • Damien, P., Wakefield, J. & Walker, S. G. (1999). “Gibbs sampling for Bayesian non-conjugate and hierarchical models by using auxiliary variables,”Journal of the Royal Statistics Society, B61, 331–344.

    MathSciNet  MATH  Google Scholar 

  • Delyon, B. (1996). “General results on the convergence of stochastic algorithms,”IEEE Transactions on Automatic Control, 46, 1245–1256.

    Article  MathSciNet  Google Scholar 

  • Dempster, A. P., Laird, N. M. & Rubin, D. B. (1977). “Maximum likelihood from incomplete data via the EM algorithm,”Journal of the Royal Statistics Society, B39, 1–38.

    MathSciNet  MATH  Google Scholar 

  • Fernandez, C, Osiewalski, J. & Steel, M. F. J. (1997). “On the use of panel data in stochastic frontier models,”Journal of Econometrics, 79, 169–193.

    Article  MathSciNet  Google Scholar 

  • Gamerman, D., 1997.Markov Chain Monte Carlo. Chapman and Hall, London.

    MATH  Google Scholar 

  • Gelfand, A. & Smith, A.F.M. (1990). “Sampling-based approaches to calculating marginal densities,”Journal of the American Statistical Association, 85, 398–409.

    Article  MathSciNet  Google Scholar 

  • Greene, W. H. (1990). “A gamma distributed stochastic frontier model,”Journal of Econometrics, 46, 141–164.

    Article  MathSciNet  Google Scholar 

  • Greene, W. H. (2000). “Simulated likelihood estimation of the normal-gamma stochastic frontier function,” Mimeo, New York University

  • Gu, M. G. & Kong, F. H. (1998). “A stochastic approximation algorithm with Markov chain Monte Carlo method for incomplete data estimation problems,”Proceeding of National Academy Sciences USA, 95, 7270–7274.

    Article  MathSciNet  Google Scholar 

  • Gu, M. G. & Zhu, H. T. (2001). “Maximum likelihood estimation for spatial models by Markov chain Monte Carlo stochastic approximation,”Journal of the Royal Statistical Society, B63, 339–355.

    Article  MathSciNet  Google Scholar 

  • Higdon, D. (1998). “Auxiliary variable methods for Markov chain Monte Carlo with applications,”Journal of the American Statistical Association, 93, 398–409.

    Article  Google Scholar 

  • Kass, R. E. & Raftery, A. E. (1995). “Bayes factors and model uncertainty,”Journal of the American Statistical Association, 90, 773–795.

    Article  MathSciNet  Google Scholar 

  • Koop, G., Steel, M. F. J. & Osiewalski, J. (1995). “Posterior analysis of stochastic frontier models using Gibbs sampling,”Computational Statistics 10, 353–373.

    MATH  Google Scholar 

  • Kumbhakar, S. C. and Lovell, C. A. K. (2000).Stochastic Frontier Analysis. Cambridge University Press.

  • Kushner, H. J. and Yin, G. G. (1997).Stochastic Approximation Algorithms and Applications. Springer, New York.

    Book  Google Scholar 

  • Liu, J. S. (2001).Monte Carlo Strategies in Scientific Computing. Springer, New York.

    MATH  Google Scholar 

  • Louis, T. A. (1982). “Finding the observed information matrix using the EM algorithm,”Journal of the Royal Statistical Society, B44, 224–233.

    MathSciNet  Google Scholar 

  • Meeusen, W. and van den Broeck, J. (1977). “Efficiency estimation from Cobb-Douglas production functions with composed error,”International Economic Review, 18, 435–444.

    Article  Google Scholar 

  • Neal, R. M. (2003). “Slice sampling,”Annals of Statistics, 31, 705–767.

    Article  MathSciNet  Google Scholar 

  • Ripley, B. D.. (1988).Stochastic Simulation. Wiley, New York.

    MATH  Google Scholar 

  • Ritter, C. & Simar, L. (1997). “Pitfalls of normal-gamma stochastic frontier models,”Journal of Productivity Analysis, 8, 167–182.

    Article  Google Scholar 

  • Robbins, H. & Monro, S. (1951). “A stochastic approximation method,”Annals of Mathematical Statistics, 22, 400–407.

    Article  MathSciNet  Google Scholar 

  • Stevenson, R. E. (1980). “Likelihood functions for generalized stochastic frontier estimation,”Journal of Econometrics, 13, 57–66.

    Article  Google Scholar 

  • Tanner, M. A. & Wong, W. H. (1987). “The calculation of posterior distributions by data augmentation,”Journal of the American Statistical Association, 82, 528–549.

    Article  MathSciNet  Google Scholar 

  • Tierney, L. (1994). “Markov chains for exploring posterior distributions,”Annals of Statistics, 22, 1701–1762.

    Article  MathSciNet  Google Scholar 

  • Tsionas, E. (2000). “Full likelihood inference in normal-gamma stochastic frontier models,”Journal of Productivity Analysis, 13, 183–196.

    Article  Google Scholar 

  • Watanabe, T. (2001). “On sampling the degree-of-freedom of Student’s-t disturbances,”Statistics & Probability Letters, 52, 177–181.

    Article  MathSciNet  Google Scholar 

  • Wei, G. C. G. & Tanner, M. A. (1990). “A Monte Carlo implementation of the EM algorithm and the poor man’s data augmentation algorithms,”Journal of the American Statistical Association, 85, 699–704.

    Article  Google Scholar 

  • Zhang, X. (1999). “A Monte Carlo study on the finite sample properties of the Gibbs sampling method for a stochastic frontier model,”Journal of Productivity Analysis, 14, 71–83.

    Article  Google Scholar 

  • Zhu, H. T. & Lee, S. Y. (2002). “Analysis of generalized linear mixed models via a stochastic approximation algorithm with Markov chain Monte-Carlo method,”Statistics and Computing, 12, 175–183.

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Graduate School of Business Administration, Kobe University, 657-8501, Kobe, Japan

    Hideo Kozumi

  2. Faculty of Economics, Okayama University, 700-8530, Okayama, Japan

    Xingyuan Zhang

Authors
  1. Hideo Kozumi
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Xingyuan Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

Additional information

The authors are grateful to two anonymous referees for their useful comments, which improved an earlier version of the paper. The first author also thanks the financial support by the Japanese Ministry of Education, Culture, Sports, Science and Technology under the Grant-in-Aid for Scientific Research No.14730022.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Kozumi, H., Zhang, X. Bayesian and non-bayesian analysis of gamma stochastic frontier models by Markov Chain Monte Carlo methods. Computational Statistics 20, 575–593 (2005). https://doi.org/10.1007/BF02741316

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02741316

Keywords