Skip to main content
SpringerLink
Log in

Belief revision by sets of sentences

  • Published:
Journal of Computer Science and Technology Aims and scope Submit manuscript

Abstract

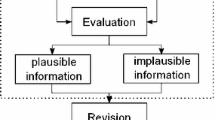
The aim of this paper is to extend the system of belief revision developed by Alchourrón, Gärdenfors and Makinson (AGM) to a more general framework. This extension enables a treatment of revision not only by single sentences but also by any sets of sentences, especially by infinite sets. The extended revision and contraction operators will be called general ones, respectively. A group of postulates for each operator is provided in such a way that it coincides with AGM's in the limit case. A notion of the nice-ordering partition is introduced to characterize the general contraction operation. A computation-oriented approach is provided for belief revision operations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Alchourrón C E, Gärdenfors P, Makinson D. On the logic of theory change: Partial meet contraction and revision functions.The Journal of Symbolic Logic, 1985, 50(2): 510–530.

    Article  MATH  MathSciNet  Google Scholar 

  2. Brewka G. Preferred subtheories: An extended logical framework for default reasoning. InProceedings of IJCAI-89, Detroit, Mich. 1989, pp.1034–1048.

  3. Brewka G. Cumulative default logic: In defense of nonmonotonic inference rules.Artificial Intelligence, 1991, 50: 183–205.

    Article  MATH  MathSciNet  Google Scholar 

  4. Boutilier C. Revision sequences and nested conditionals. InProceedings of IJCAI-95, pp.519–525, 1993.

  5. Boutilier C. Unifying default reasoning and belief revision in a modal framework.Artificial Intelligence, 1994, 68: 33–85.

    Article  MATH  MathSciNet  Google Scholar 

  6. Cerro L F, Herzig A, Lang J. From ordering-based nonmonotonic reasoning to conditional logic.Artificial Intelligence, 1994, 66: 375–393.

    Article  MATH  MathSciNet  Google Scholar 

  7. Dubois D, Prade H. Epistemic entrenchment and possibilistic logic.Artificial Intelligence, 1991, 50: 223–239.

    Article  MATH  MathSciNet  Google Scholar 

  8. Fuhrmann A. On the modal logic of theory change. InThe Logic of Theory Change (Lecture Notes in Computer Science 465), Fuhrmann A, Morreau M (eds.), Springer-Verlag, 1991, pp.259–281.

  9. Fuhrmann A, Hansson S O. A survey of multiple contractions.Journal of Logic, Language, and Information, 1994, 3: 39–76.

    Article  MathSciNet  Google Scholar 

  10. Gärdenfors P. Propositional logic based on the dynamics of belief.The Journal of Symbolic Logic 1985, 50(2): 390–394.

    Article  MATH  MathSciNet  Google Scholar 

  11. Gärdenfors P. Knowledge in Flux: Modeling the Dynamics of Epistemic States. The MIT Press, 1988.

  12. Gärdenfors P, Makinson D. Nonmonotonic inference based on expectations.Artificial Intelligence, 1994, 65: 197–245.

    Article  MATH  MathSciNet  Google Scholar 

  13. Hansson S O. A dyadic representation of belief. InBelief Revision Gärdenfors P (ed.), Cambridge University Press, Cambridge, 1992, pp.89–121.

    Google Scholar 

  14. Hansson S O. Theory contraction and base contraction unified.The Journal of Symbolic Logic, 1993, 58(2): 602–625.

    Article  MATH  MathSciNet  Google Scholar 

  15. Hansson S O. Reversing the Levi identityJournal of Philosophical Logic 1993, 22: 637–669.

    Article  MATH  MathSciNet  Google Scholar 

  16. Hájek P. Epistemic entrenchment and arithmetical hierarchy.Artificial Intelligence, 1991, 62: 79–87.

    Article  Google Scholar 

  17. Jech T. Set Theory. Academic Press, New York, 1978.

    Google Scholar 

  18. Katsuno H, Mendelzon A O. Propositional knowledge base revision and minimal change.Artificial Intelligence, 1991, 52: 203–294.

    Article  MathSciNet  Google Scholar 

  19. Makinson D, Gärdenfors P. Relations between the logic of theory change and nonmonotonic logic. InThe Logic of Theory Change, (Lecture Notes in Computer Science 465), Fuhrmann A, Morreau M (eds.), Springer-Verlag, Berlin, Germany, 1991, pp.185–205.

    Google Scholar 

  20. Nebel B. Reasoning and Revision in Hybrid Representation System (Lecture Notes in Artificial Intelligence 422). Springer-Verlag, 1990.

  21. Nebel B. Syntax based approaches to belief revision. InBelief Revision, Gärdenfors P (ed.), Cambridge University Press, Cambridge, 1992, 52–88.

    Google Scholar 

  22. Niederèe R. Multiple contraction: A further case against Gärdenfors' principle of recovery. InThe Logic of Theory Change (Lecture Notes in Computer Science 465), Fuhrmann A, Morreau M (eds.), Springer-Verlag, 1991, pp.322–334.

  23. Rott H. On the logic of theory change: More maps between different kinds of contraction function. InBelief Revision, Gärdenfors P (ed.), Cambridge University Press, Cambridge, 1992, pp. 122–140.

    Google Scholar 

  24. Rott H. Belief contraction in the context of the general theory of rational choice.The Journal of Symbolic Logic, 1993, 58(4): 1426–1450.

    Article  MATH  MathSciNet  Google Scholar 

  25. Weydert E. Relevance and revision: About generalizing syntax-based belief revision. InEuropean Workshop JELIA'92 (Lecture Notes in Artificial Intelligence 633), Pearce D, Wagner G (eds.), Springer-Verlag, Berlin, 1992, pp. 126–138.

    Google Scholar 

  26. Zhang Dongmo. A general framework for belief revision. InProc. of 4th Int'l Conf. for Young Computer Scientists, Peking University Press, 1995, 574–581.

Download references

Author information

Authors and Affiliations

  1. Department of Computer Science, Nanjing University of Aeronautics and Astronautics, 210016, Nanjing

    Zhang Dongmo

Authors
  1. Zhang Dongmo
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Zhang Dongmo.

Additional information

This work was partly supported by the High-Tech R/D Program of China.

Zhang Dongmo received a Diploma in mathematics from Nanjing Normal University in 1980 and his M.S. degree in computer application from Nanjing University of Aeronautics and Astronautics (NUAA) in 1992. He has been on the faculty of the Department of Computer Science at NUAA since 1993 and is a Ph.D. candidate at Institute of Computer Science at NUAA. His research interets include mathematical logic, automated reasoning, knowledge representation and reasoning and distributed artificial intelligence.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Zhang, D. Belief revision by sets of sentences. J. of Comput. Sci. & Technol. 11, 108–125 (1996). https://doi.org/10.1007/BF02943527

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02943527

Keywords

Search

Navigation