Abstract
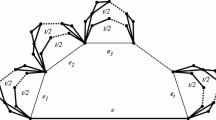
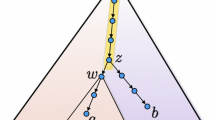
A graph is self-repairing if it is 2-connected and such that the removal of any single vertex results in no increase in distance between any pair of remaining vertices of the graph. We completely characterize the class of minimum self-repairing graphs, which have the fewest edges for a given number of vertices.
Similar content being viewed by others
References
Arnborg, S., and Proskurowski, A.: Linear time algorithms for NP-hard problems restricted to partial k-trees. Discrete Applied Mathematics 23, 11–24 (1989)
Dawes, R.: Minimally 3-connected graphs, J. of Comb. Theory, Ser. B, 40, 159–167 (1986)
Farley, A.M., Proskurowski, A.: “Reliable minimum-time broadcast networks”, Proc. of 18th Southeastern Conference on Combinatorics, Graph Theory, and Computing, Congressus Numerantium 59. pp. 37–48, 1987
Farley, A.M., Proskurowski, A.: Self-repairing networks. Parallel Processing Letters 3(4), 381–391 (1994)
Harary, F., Graph theory, Addison-Wesley, Reading, Mass, 1969
Hedetniemi, S.T.: Characterizations and constructions of minimally 2-connected graphs and minimally strong digraphs, in Proc. 2nd. Louisiana Conf. on Combinatorics, Graph Theory and Computing. pp. 76–85. Winnipeg: Utilitas Mathematica 1979
Robertson, N., Seymour, P.D.: Graph Minors II: Algorithmic aspects of treewidth. J. Algorithms 7, 39–61 (1986)
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Farley, A.M., Proskurowski, A. Minimum Self-Repairing Graphs. Graphs and Combinatorics 13, 345–351 (1997). https://doi.org/10.1007/BF03353012
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/BF03353012