Abstract
Let G and H be two simple undirected graphs. An embedding of the graph G in the graph H is an injective mapping f from the vertices of G into the vertices of H together with a mapping Pf of edges of G into paths in H. The dilation of the embedding is the maximum taken over all the lengths of the paths Pf(x,y) associated with the edges (x,y) of G.
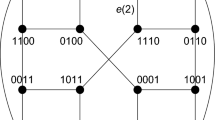
One challenge pointed out in [9] is to find embeddings of the de Bruijn graph in the hypercube of the same order which have a low dilation. For a de Bruijn graph of diameter D we give an embedding in a hypercube of the same diameter of dilation 2[D/51], and determine the edge-congestion and vertex-congestion of this embedding. Similar results are given for the shuffle-exchange graphs.
The work was supported partially by NSERC of Canada and by PRC C3 of France and was partially done while the third author was visiting the University of Paris-Sud.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
J.-C. Bermond and C. Peyrat. de Bruijn and Kautz networks: a competitor for the hypercube? Proceedings of the 1st European Workshop on Hypercubes and Distributed Computers, Rennes, North Holland, F.Andre aced J.P. Verjus ed.,pages 279–293, 1989.
S. Bhatt, F. Chung, T. Leighton, and A. Rosenberg. Optimal simulations of tree machines. IEEE, pages 274–282, 1986.
M. Bouabdallah and J.-C. Konig. Embedding de Bruijn networks in the hypercube. Preprint, 1990.
M. Chan. Embedding of d-dimensional grids into optimal hypercubes. 1st ACM Symposium on Parallel Algorithms and Architectures, pages 52–57, 1989.
O. Collins, S. Dolinar, R. McEliece, and F. Pollara. A VLSI decomposition of the de Bruijn graph. Preprint, 1989.
N. de Bruijn. A combinatorical problem. Koninklijke Nederlandsche Akademie van Wetenschappen Proc., A 49: 758–764, 1946.
R. Feldmann and W. Unger. The cube connected cycle network is a subgraph of the butterfly network. Technical report, University of Paderborn, 1991.
D. Greenberg and S. Bhatt. Routing multiple paths in hypercubes. Proceedings of SPAA, pages 45–54, 1990.
D. S. Greenberg, L. S. Heath, and A. Rosenberg. Optimal embeddings of butterfly-like graphs in the hypercube. Mathematical Systems Theory, 23: 61–77, 1990.
C.-T. Ho and S. L. Johnson. Embedding meshes in boolean cubes by graph decomposition. Journal of Parallel and Distributed Computing, 8: 325–339, 1990.
R. Koch, T. Leighton, B. Maggs, S. Rao, and A. Rosenberg. Work-preserving emulations of fixed-connection networks. Preprint.
B. Monien and H. Sudborough. Comparing interconnection networks. Preprint, 1988.
E. J. Schwabe. On the computational equivalence of hypercube-derived networks. 2nd Symposium on Parallel Algorithms and Architectures, pages 388–397, 1990.
P. M. Winkler. The metric structure of graphs. Surveys in Combinatorics, (C. Whitehead, ed.), London Math. Soc. Lecture Notes Series, 123:197–221, 1987.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 1991 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Baumslag, M., Heydemann, M.C., Opatrny, J., Sotteau, D. (1991). Embeddings of shuffle-like graphs in hypercubes. In: Aarts, E.H.L., van Leeuwen, J., Rem, M. (eds) Parle ’91 Parallel Architectures and Languages Europe. Lecture Notes in Computer Science, vol 505. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-25209-3_13
Download citation
DOI: https://doi.org/10.1007/978-3-662-25209-3_13
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-23206-4
Online ISBN: 978-3-662-25209-3
eBook Packages: Springer Book Archive