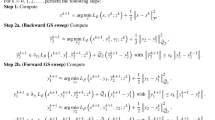Abstract
In this paper, an efficient algorithm is proposed to design nearly-perfect-reconstruction (NPR) DFT-modulated filter banks. First, the perfect-reconstruction (PR) condition of the oversampled DFT-modulated filter banks in the frequency domain is transformed into a set of quadratic equations with respect to the prototype filter (PF) in the time domain. Second, the design problem is formulated as an unconstrained optimization problem that involves PR condition and stopband energy of the PF. With the gradient vector of the objective function, an efficient iterative algorithm is presented to design the PF, which is updated with linear matrix equations at each iteration. The algorithm is identified as a modified Newton’s method, and its convergence is proved. Numerical examples and comparison with many other existing methods are included to demonstrate the effectiveness of the proposed method.




Similar content being viewed by others
References
Z. Cvetkovic, M. Vetterli, Tight Weyl–Heisenberg frames in ℓ 2(Z). IEEE Trans. Signal Process. 46(5), 1256–1259 (1998)
H.H. Dam, S. Nordholm, A. Cantoni, J.M. de Haan, Iterative method for the design of DFT filter bank. IEEE Trans. Circuits Syst. II, Analog Digit. Signal Process. 51(11), 581–586 (2004)
B. Dumitrescu, R. Bregovi, T. Saramki, Simplified design of low-delay oversampled NPR GDFT filterbanks. EURASIP J. Appl. Signal Process. 2006, 42961 (2006)
Y.T. Fong, C.W. Kok, Iterative least squares of DC-leakage free paraunitary cosine modulated filter banks. IEEE Trans. Circuits Syst. II, Analog Digit. Signal Process. 50(5), 238–243 (2003)
X.Q. Gao et al., An efficient digital implementation of multicarrier CDMA system based on generalized DFT filter banks. IEEE J. Sel. Areas Commun. 24(6), 1189–1198 (2006)
T.Q. Nguyen, Digital filter bank design quadratic-constrained formulation. IEEE Trans. Signal Process. 43(9), 2103–2108 (1995)
I.W. Selesnick, R.G. Baraniuk, N.G. Kingsbury, The dual-tree complex wavelet transform. IEEE Signal Process. Mag. 22(6), 123–151 (2005)
P.L. Shui, Image denoising using 2-D oversampled DFT modulated filter banks. IET Image Process. 3(3), 163–173 (2009)
P.L. Shui, J.Z. Jiang, X.L. Wang, Design of oversampled double-prototype DFT modulated filter banks via bi-iterative second-order cone program. Signal Process. 90(5), 1597–1608 (2010)
W.Y. Sun, Y.X. Yuan, Optimization Theory and Methods: Nonlinear Programming (Springer, Berlin, 2006)
P.P. Vaidyanathan, Multirate Systems and Filterbanks (Prentice-Hall, Englewood Cliffs, 1993)
S. Weiss, R.W. Stewart, Fast implementation of oversampled modulated filter banks. Electron. Lett. 30(17), 1502–1503 (2000)
M.R. Wilbur, T.N. Davidson, J.P. Reilly, Efficient design of oversampled NPR GDFT filterbanks. IEEE Trans. Signal Process. 52(7), 1947–1963 (2004)
K.F.C. Yiu et al., Multicriteria design of oversampled uniform DFT filter banks. IEEE Signal Process. Lett. 11(6), 541–544 (2004)
Z.J. Zhang, Efficient design of cosine modulated filter banks based on gradient information. IEEE Signal Process. Lett. 14(12), 940–943 (2007)
Acknowledgements
The authors would like to thank the anonymous reviewers and the Associate Editor for their valuable comments and suggestions, which have greatly improved the quality of this paper. This work is supported by the National Natural Science Foundation of China (Granted No. 61261032, No. 60972084) and Guangxi Science Foundation (Granted No. 05112001-7A, No. 0832007Z).
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Proof of Property 3.1
Let G(h)=A(h)h. Then the objective function can be written as a function of G(h) and h:

Similar to that in [15], the derivative of G T(h) with respect to h is
where I N is the N×N identity matrix, and ⊗ denotes the Kronecker product. As a result, the gradient vector can be derived by

The proof is completed. □
Appendix B: Efficient calculation of A T(h 0)
From the definition of matrices  , the matrix A
T(h
0) can be calculated without using any matrix-vector multiple. Given k,l,r
i
, we obtain
, the matrix A
T(h
0) can be calculated without using any matrix-vector multiple. Given k,l,r
i
, we obtain

In (30), \(\mathbf{h}_{0}^{T}\mathbf{U}_{l_{0}}\mathbf{D}_{n}\mathbf{U}_{l_{1}}^{T}\) can be fast calculated with the following three steps:
-
(1)
In terms of (10), \(\mathbf{d}_{l_{0}} = \mathbf{h}_{0}^{T}\mathbf{U}_{l_{0}}\) is calculated by decimating \([\mathbf{h}_{0}^{T},\mathbf{0}^{T}]\) with offset factor l 0, where 0 is the (P−2)×1 zero vector, and the zero padding is performed to make \(\mathbf{d}_{l_{0}}\) have the same size for different l 0.
-
(2)
The matrix D n is a highly sparse matrix, with the coordinates of its nonzero entries, \(\mathbf{d}_{l_{0},n} = \mathbf{h}_{0}^{T}\mathbf{U}_{l_{0}}\mathbf{D}_{n}\) can be quickly formed without any multiple.
-
(3)
Interpolating \(\mathbf{d}_{l_{0},n}\) with offset factor l 1 to form a 1×((m+1)P−1) vector g, we have \(\mathbf{h}_{0}^{T}\mathbf{U}_{l_{0}}\mathbf{D}_{n}\mathbf{U}_{l_{1}}^{T} = [g(1), \ldots,g(mP + 1)]\), which is sparsely represented in numerical simulation.
As a result, the row vector  can be efficiently calculated only with several additions. Then A
T(h
0) is formed by orderly stacking
can be efficiently calculated only with several additions. Then A
T(h
0) is formed by orderly stacking  with different k,l,r
i
. □
with different k,l,r
i
. □
Rights and permissions
About this article
Cite this article
Jiang, J., Ouyang, S. & Zhou, F. Design of NPR DFT-Modulated Filter Banks via Iterative Updating Algorithm. Circuits Syst Signal Process 32, 1351–1362 (2013). https://doi.org/10.1007/s00034-012-9515-x
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00034-012-9515-x