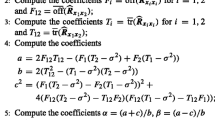Skip to main content

Advertisement

Springer Nature Link
Log in

Multidimensional Blind Separation Using Higher-Order Statistics: Application to Non-Cooperative STBC Systems

  • Published:
Circuits, Systems, and Signal Processing Aims and scope Submit manuscript

Abstract

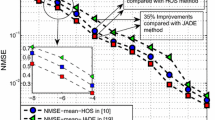
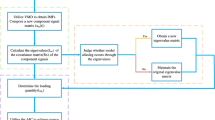
Blindly separating the intercepted signals is a challenging problem in non-cooperative multiple input multiple output systems in association with space–time block code (STBC) where channel state information and coding matrix are unavailable. To our knowledge, there is no report on dealing with this problem in literature. In this paper, the STBC systems are represented with an independent component analysis (ICA) model by merging the channel and coding matrices as virtual channel matrix. Analysis shows that the source signals are of group-wise independence and the condition of mutual independence can not be satisfied for ordinary ICA algorithms when specific modulations are employed. A new multidimensional ICA algorithm is proposed to separate the intercepted signals in this case by jointly block-diagonalizing (JBD) the cumulant matrices. In this paper, JBD is achieved by a 2-step optimization algorithm and a contrast function is derived from the JBD criterion to remove the additional permutation ambiguity with explicit mathematical explanations. The convergence of the new method is guaranteed. Compared with the ICA-based channel estimation methods, simulations show that the new algorithm, which does not introduce additional ambiguities, achieves better performance with faster convergence in a non-cooperative scenario.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. K. Abed-Meraim, A. Belouchrani, Algorithms for joint block diagonalization, in Proceedings of the EUSIPCO, 2004, pp. 209–212

  2. T.E. Abrudan, J. Eriksson, V. Koivunen, Steepest descent algorithms for optimization under unitary matrix constraint. IEEE Trans. Signal. Process. 56(3), 1134–1147 (2008)

    Article  MathSciNet  Google Scholar 

  3. S. Alamouti, A simple transmit diversity technique for wireless communications. IEEE J. Sel. Areas Commun. 16(8), 1451–1458 (1998)

    Article  Google Scholar 

  4. S. Amari, A. Cichocki, H.H. Yang, A new learning algorithm for blind signal separation. Adv. Neural Inf. Process. Syst. 8, 757–763 (1996)

    Google Scholar 

  5. S. Aouada, A. Zoubir. C. See, A comparative study on source number detection, in IEEE ISSPA, 2003, pp. 173–176

  6. A. Belouchrani, K. Abed-Meraim, J. Cardoso, E. Moulines, A blind source separation technique using second-order statistics. IEEE Trans. Signal Process. 45(2), 434–444 (2002)

    Article  Google Scholar 

  7. T. Blaschke, L. Wiskott, CuBICA: independent component analysis by simultaneous third-and fourth-order cumulant diagonalization. IEEE Trans. Signal Process. 52(5), 1250–1256 (2004)

    Article  MathSciNet  Google Scholar 

  8. J.F. Cardoso, Source separation using higher order moments, in IEEE ICASSP, 1989, pp. 2109–2112

  9. J.F. Cardoso, Eigen-structure of the fourth-order cumulant tensor with application to the blind source separation problem, in IEEE ICASSP, 1990, pp. 2655–2658

  10. J.F. Cardoso, Multidimensional independent component analysis, in IEEE ICASSP, 1998, pp. 1941–1944

  11. J.F. Cardoso, A. Souloumiac, Blind beamforming for non-Gaussian signals, in IEE Proceedings of the Radar and Signal Processing, 1993, pp. 362–370

  12. J.F. Cardoso, A. Souloumiac, Jacobi angles for simultaneous diagonalization. SIAM J. Matrix Anal. Appl. 17(1), 161–164 (1996)

    Article  MATH  MathSciNet  Google Scholar 

  13. V. Choqueuse, K. Yao, L. Collin, G. Burel, Hierarchical space–time block code recognition using correlation matrices. IEEE Trans. Wireless Commun. 7(9), 3526–3534 (2008)

    Article  Google Scholar 

  14. V. Choqueuse, M. Marazin, L. Collin, K.C. Yao, G. Burel, Blind recognition of linear space–time block codes: a likelihood-based approach. IEEE Trans. Signal Process. 58(3), 1290–1299 (2010)

    Article  MathSciNet  Google Scholar 

  15. V. Choqueuse, A. Mansour, G. Burel, L. Collin, K. Yao, Blind channel estimation for STBC systems using higher-order statistics. IEEE Trans. Wireless Commun. 10(2), 495–505 (2011)

    Article  Google Scholar 

  16. P. Ciblat, P. Loubaton, E. Serpedin, G. Giannakis, Asymptotic analysis of blind cyclic correlation-based symbol-rate estimators. IEEE Trans. Inf. Theory 48(7), 1922–1934 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  17. P. Comon, Independent component analysis, a new concept? Signal Process. 36(3), 287–314 (1994)

    Article  MATH  Google Scholar 

  18. P. Comon, B. Mourrain, Decomposition of quantics in sums of powers of linear forms. Signal Process. 53(2), 93–107 (1996)

    Article  MATH  Google Scholar 

  19. L. De Lathauwer, J. Castaing, J.-F. Cardoso, Fourth-order cumulant-based blind identification of underdetermined mixtures. IEEE Trans. Signal Process. 55(6), 2965–2973 (2007)

    Article  MathSciNet  Google Scholar 

  20. C. Févotte, F.J. Theis, Orthonormal approximate joint block-diagonalization, Technique report. GET/Télécom, Paris, 2007

  21. G. Ganesan, P. Stoica, Space–time block codes: a maximum SNR approach. IEEE Trans. Inf. Theory 47(4), 1650–1656 (2002)

    Article  MathSciNet  Google Scholar 

  22. K. Hassan, I. Dayoub, W. Hamouda, C.N. Nzeza, M. Berbineau, Blind digital modulation identification for spatially-correlated MIMO systems. IEEE Trans. Wireless Commun. 11(2), 683–693 (2012)

    Article  Google Scholar 

  23. B. Hassibi, B.M. Hochwald, High-rate codes that are linear in space and time. IEEE Trans. Inf. Theory 48(7), 1804–1824 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  24. A. Hyvärinen, J. Karhunen, E. Oja, Independent Component Analysis (Wiley, New York, 2001)

    Book  Google Scholar 

  25. IEEE 802.16e, standard for local and metropolitan area networks, part 16: air interface for fixed and mobile broadband wireless access system, 2005

  26. H. Jafarkhani, A quasi-orthogonal space–time block code. IEEE Trans. Commun. 49(1), 1–4 (2001)

    Article  MATH  Google Scholar 

  27. E. Larsson, P. Stoica, Space–Time Block Coding for Wireless Communications (Cambridge University Press, Cambridge, 2003)

    Book  MATH  Google Scholar 

  28. E. Larsson, P. Stoica, J. Li, Orthogonal space–time block codes: maximum likelihood detection for unknown channels and unstructured interferences. IEEE Trans. Signal Process. 51(2), 362–372 (2003)

    Article  MathSciNet  Google Scholar 

  29. M. Luo, L. Li. B. Tang, A blind modulation recognition algorithm suitable for MIMO–STBC systems, in IEEE CIT, 2012, pp. 271–276

  30. A. Mansour, J. Youssef. K.-C. Yao, Underdetermined bss of miso ostbc signals, in Springer Independent Component Analysis and Signal Separation, 2009, pp. 678–685

  31. J. Mendel, Tutorial on higher-order statistics (spectra) in signal processing and system theory: theoretical results and some applications. Proc. IEEE. 79(3), 278–305 (2002)

    Article  MathSciNet  Google Scholar 

  32. E. Moulines, J.F. Cardoso, Second-order versus fourth-order MUSIC algorithms: an asymptotical statistical analysis, in IEEE Signal Process Workshop on Higher-Order, Statistics, 1991, pp. 121–130

  33. S. Shahbazpanahi, A.B. Gershman, J.H. Manton, Closed-form blind MIMO channel estimation for orthogonal space–time block codes. IEEE Trans. Signal Process. 53(12), 4506–4517 (2005)

    Article  MathSciNet  Google Scholar 

  34. A.L. Swindlehurst, G. Leus, Blind and semi-blind equalization for generalized space–time block codes. IEEE Trans. Signal Process. 50(10), 2489–2498 (2002)

    Article  Google Scholar 

  35. V. Tarokh, H. Jafarkhani, A.R. Calderbank, Space–time block codes from orthogonal designs. IEEE Trans. Inf. theory. 45(5), 1456–1467 (1999)

    Article  MATH  MathSciNet  Google Scholar 

  36. F.J. Theis, Towards a general independent subspace analysis, in MIT, Advances in Neural Information Processing Systems, 2007, pp. 1361–1369

  37. B. Vucetic, J. Yuan, Space–Time Coding (Wiley, New York, 2003)

    Book  Google Scholar 

  38. M. Wax, T. Kailath, Detection of signals by information theoretic criteria. IEEE Trans. Acoust. Speech Signal Process. 33(2), 387–392 (1985)

    Article  MathSciNet  Google Scholar 

  39. W. Yik-Chung, C. Shing-Chow, On the symbol timing recovery in space-time coding systems, in IEEE WCNC, 2003, pp. 420–424

  40. H. Zhang, L. Li, W. Li, Independent component analysis based on fast proximal gradient. Circuits Syst. Signal Process. 31(2), 583–593 (2012)

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Electronic Engineering, University of Electronic Science and Technology of China, Chengdu,  611731, China

    Minggang Luo, Liping Li, Guobing Qian & Hongshu Liao

  2. School of Mathematics and Computer Science, Panzhihua University, Panzhihua,  617000, China

    Minggang Luo

Authors
  1. Minggang Luo
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Liping Li
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Guobing Qian
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Hongshu Liao
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Minggang Luo.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Luo, M., Li, L., Qian, G. et al. Multidimensional Blind Separation Using Higher-Order Statistics: Application to Non-Cooperative STBC Systems. Circuits Syst Signal Process 33, 2173–2192 (2014). https://doi.org/10.1007/s00034-014-9738-0

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00034-014-9738-0

Keywords