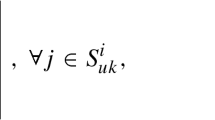Abstract
This article aims to investigate the problem of robust finite-time output feedback \( H_\infty \) control for stochastic jump systems with incomplete transition rates. Firstly, for the nominal stochastic jump systems, the sufficient conditions for the finite-time boundedness and finite-time output feedback stabilization are developed, respectively. Then, a robust finite-time \( H_\infty \) output feedback controller is designed by means of linear matrix inequalities. A key point of this work is to relax the special requirement of completely known transition rates to more general form that mixes two cases of completely known and completely unknown transition rates. Finally, a numerical example is given to demonstrate the applicability of the main results.




Similar content being viewed by others
References
F. Amato, M. Ariola, P. Dorato, Finite-time control of linear systems subject to parametric uncertainties and disturbances. Automatica 37(9), 1459–1463 (2001)
M. Athans, Command and control theory: a challenge to control science. IEEE Trans. Autom. Control 32(4), 286–293 (1987)
E.K. Boukas, Static output feedback control for stochastic hybrid systems: LMI approach. Automatica 42(1), 183–188 (2006)
W.H. Chen, J.X. Xu, Z.H. Guan, Guaranteed cost control for uncertain Markovian jump systems with mode-dependent time-delays. IEEE Trans. Autom. Control 48(12), 2270–2277 (2003)
M. Darouach, M. Chadli, Admissibility and control of switched discrete-time singular systems. Syst. Sci. Control Eng. 1(1), 43–51 (2013)
H.L. Dong, Z.D. Wang, W.C.H. Daniel, H.J. Gao, Robust \(H_\infty \) filtering for Markovian jump systems with randomly occurring nonlinearities and sensor saturation: the finite-horizon case. IEEE Trans. Signal Process. 59(7), 3048–3057 (2011)
H.L. Dong, Z.D. Wang, H.J. Gao, Distributed \(H_\infty \) filtering for a class of Markovian jump nonlinear time-delay systems over lossy sensor networks. IEEE Trans. Ind. Electron. 60(10), 4665–4672 (2013)
P. Dorato, Short time stability in linear time-varying systems, in Proceedings of the IRE International Convention, Record Part 4, pp. 83–87. New York, USA (1961).
Z.Y. Fei, H.J. Gao, P. Shi, New results on stabilization of Markovian jump systems with time delay. Automatica 45(10), 2300–2306 (2009)
H.J. Gao, X.Y. Meng, T.W. Chen, L. James, Stabilization of networked control systems via dynamic output-feedback controllers. SIAM J. Control Optim. 48(5), 3643–3658 (2010)
L.L. Hou, G.D. Zong, W.X. Zheng, Y.Q. Wu, Exponential \(l_2-l_\infty \) control for discrete-time switching Markov jump linear systems. Circuits Syst. Signal Process. 32(2), 2745–2759 (2013)
Z.W. Lin, J.Z. Liu, W.H. Zhang, Y.G. Niu, Stabilization of interconnected nonlinear stochastic Markovian jump systems via dissipativity approach. Automatica 47(12), 2796–2800 (2011)
F. Liu, Y. Cai, Passive analysis and synthesis of Markovian jump systems with norm bounded uncertainty and unknown delay. Dyn. Contin. Discret. Ser. A 13A(1), 157–166 (2006)
M. Liu, D.W.C. Ho, Y.G. Niu, Stabilization of Markovian jump linear system over networks with random communication delay. Automatica 45(2), 416–421 (2009)
R.Q. Lu, B. Lou, A.K. Xue, Mode-dependent quantised \(H_\infty \) filtering for Markovian jump singular system. Int. J. Syst. Sci. (2013). doi:10.1080/00207721.2013.837539
X.L. Luan, F. Liu, P. Shi, Robust finite-time control for a class of extended stochastic switching systems. Int. J. Syst. Sci. 42(7), 1197–1205 (2011)
X.R. Mao, Stability of stochastic differential equations with Markovian switching. Stoch. Process. Appl. 79(1), 45–67 (1999)
L.J. Shen, U. Buscher, Solving the serial batching problem in job shop manufacturing systems. Eur. J. Oper. Res. 221(1), 14–26 (2012)
X.M. Sun, G.P. Liu, D. Reeds, W. Wang, Controller failure analysis for systems with time-varying delay. IEEE Trans. Autom. Control 53(10), 2391–2396 (2008)
Z.D. Wang, H. Qiao, K.J. Burnham, On stabilization of bilinear uncertain time-delay stochasticsystems with Markovian jumping parameters. IEEE Trans. Autom. Control 47(4), 640–646 (2002)
Y.Y. Wang, L.H. Xie, C.E. Souza, Robust control of a class of uncertain nonlinear systems. Syst. Control Lett. 19(2), 139–149 (1992)
L. Weiss, E.F. Infante, Finite-time stability under perturbing forces and on product spaces. IEEE Trans. Autom. Control 12(1), 54–59 (1967)
H.N. Wu, K.Y. Cai, Mode-independent robust stabilization for uncertain Markovian jump nonlinear systems via fuzzy control. Syst. Man Cybern. Part B Cybern. 36(3), 509–519 (2006)
Z.J. Wu, Y.H. Liu, Robust output-feedback control for stochastic nonlinear systems with modeling errors. J. Control Theory Appl. 10(3), 344–348 (2012)
Z.G. Wu, P. Shi, H.Y. Su, J. Chu, Passivity analysis for discrete-time stochastic Markovian jump neural networks with mixed time-delays. IEEE Trans. Neural Netw. 22(10), 1566–1575 (2011)
Z.G. Wu, P. Shi, H.Y. Su, J. Chu, Stochastic synchronization of Markovian jump neural networks with time-varying delay using sampled-data. IEEE Trans. Cybern. 43(6), 1796–1806 (2013)
Z.G. Wu, P. Shi, H.Y. Su, J. Chu, Asynchronous \(l_2-l_\infty \) filtering for discrete-time stochastic Markov jump systems with randomly occurred sensor nonlinearities. Automatica 50(1), 180–186 (2014)
H. Wu, W. Wang, H. Ye, Z.D. Wang, State estimation for Markovian jump linear systems with bounded disturbances. Automatica 49(11), 3292–3303 (2013)
L.G. Wu, X.M. Yao, W.X. Zheng, Generalized fault detection for two-dimensional Markovian jump systems. Automatica 48(8), 1741–1750 (2012)
L.X. Zhang, E.K. Boukas, Stability and stabilization of Markovian jump linear systems with partly unknown transition probabilities. Automatica 45(2), 463–468 (2009)
Y. Zhang, Y. He, M. Wu, J. Zhang, Stabilization for Markovian jump systems with partial information on transition probability based on free-weighting matrices. Automatica 47(1), 79–84 (2011)
Y.S. Zhang, S.Y. Xu, J.H. Zhang, Delay-dependent robust \(H_\infty \) control for uncertain fuzzy Markovian jump systems. Int. J. Control Autom. 7(4), 520–529 (2009)
G.D. Zong, D. Yang, L.L. Hou, Q.Z. Wang, Robust finite-time \(H_\infty \) control for Markovian jump systems with partially known transition probabilities. J. Frankl. Inst. 350(6), 1562–1578 (2013)
Acknowledgments
This work was supported by the National Natural Science Foundation of China under Grants 61233002 and 61174073and IAPI Fundamental Research Funds under Grant 2013ZCX03-01.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
1.1 Proof of Lemma 2
Proof
For the stochastic jump system (1) (\(u(t)=0, v(t)=0\), and \(F(t, r_t)=0\)), choose a Lyapunov function candidate as (30). Then, by Definition 4, we obtain
If the transition rates are not accessible completely, the following equation hold for arbitrary symmetric matrices \(Q_i\) due to \(\sum _{j=1}^N{\pi _{ij}}Q_i=0\)
If \(i\in L_k^i\)(the elements of the diagonal are known), by inequalities (14) and (15), the following inequality holds
If \(i\in L_{uk}^i\)(the elements of the diagonal are unknown), according to inequalities (14–16), the inequality (63) holds. Multiplying (63) by \(e^{-\alpha t}\) yields
According to Dynkin’s formula for (64), we get
which shows
This together with \(\tilde{P}_i={H_i^{-1/2}}P_i{H_i^{-1/2}}\) gives rise to
Consider
For \(\forall t\in [0, T]\), we obtain
This completes the proof. \(\square \)
1.2 Proof of Lemma 3
Proof
For the stochastic jump system (1) (\(u = 0\) and \(F(t, r_t)=0\)), choose a Lyapunov function candidate as (30). Based on Definition 4, we have
Since \(\sum _{j=1}^N{\pi _{ij}}Q_i=0\) is always true for arbitrary symmetric matrices \(Q_i\), (70) can be rewritten as
Notice that \(\pi _{ij}\ge 0\) for all \(i\ne j\), and \(\pi _{ii}=-\displaystyle {}{\sum _{j=1,i\ne j}^{N}}{\pi _{ij}}<0\) for all \(i\in \mathcal {M}\), if \(i\in L_k^i\) (the elements of the diagonal are known), by inequalities (18) and (19), the following inequality holds
If \(i\in L_{uk}^i\)(the elements of the diagonal are unknown), according to inequalities (18–20), the inequality (72) holds. Multiplying (72) by \(e^{-\alpha t}\) yields
Using Dynkin’s formula to (73), we obtain
which in turn shows
This together with \(\tilde{P}_i={H_i^{-1/2}}P_i{H_i^{-1/2}}\) gives rise to
Taking into account the fact that
\(\forall t\in [0, T]\), we have
This completes the proof. \(\square \)
Rights and permissions
About this article
Cite this article
Yang, D., Zhao, J. Robust Finite-Time Output Feedback \( H_\infty \) Control for Stochastic Jump Systems with Incomplete Transition Rates. Circuits Syst Signal Process 34, 1799–1824 (2015). https://doi.org/10.1007/s00034-014-9941-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00034-014-9941-z