Abstract
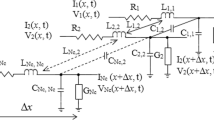
This paper presents novel methods for modeling and analysis of on-chip Single and H-tree distributed resistance inductance capacitance interconnects. The matrix pade-type approximation and scaling and squaring methods are employed for the numerical estimation of delay in single interconnect, and H-tree interconnects. The proposed models, which are based on these methods, provide rational function approximation for obtaining a passive interconnect model. Multiple single input single output model approximated transfer functions are developed for H-tree interconnects structure. With the equivalent reduced order lossy interconnect transfer functions, finite ramp responses are obtained, and line delay is estimated for various line lengths, input ramp rise times, source resistances, parasitic capacitances and load capacitances. In order to demonstrate the accuracy of proposed models, the estimated 50 % delay values are compared with the standard HSPICE W-element model and are found to be in good agreement. The proposed models worst case 50 % delay errors of single interconnect are 0.27 and 0.24 % respectively, while the worst case 50 % delay errors of H-tree structure are 5.73 and 3.94 % respectively.










Similar content being viewed by others
References
K. Banerjee, A. Mehrotra, Analysis of on-chip inductance effects for distributed RLC interconnects. IEEE Trans. CAD. 21(8), 904–915 (2002)
C. Brezinski, Rational approximation to formal power series. J. Approx. Theory 25(4), 295–317 (1979)
C. Brezinski, Padé-Type Approximation and General Orthogonal Polynomials (Birkh Äauser-Verlag, Basel, 1980)
I. Chanodia, D. Velenis, Parameter variations and crosstalk noise effects on high performance H-tree clock distribution networks. Analog Integr. Circuits Signal Process. 56(1–2), 13–21 (2008)
A. Draux, Approximants de Type Padé et de Table. Little: Publication A, University of Lille, Lille, No. 96 (1983)
W.C. Elmore, The transient response of damped linear networks with particular regard to wideband amplifiers. J. Appl. Phys. 19(1), 55–63 (1948)
M.A. El-Moursy, E.G. Friedman, Exponentially tapered H-tree clock distribution networks. IEEE Trans. VLSI Syst. 13(8), 971–975 (2005)
T. Eudes, B. Ravelo, Analysis of multi-gigabits signal integrity through clock H-tree. Int. J. Circuit Theory Appl. 41(4), 535–549 (2012)
E.G. Friedman (ed.), High Performance Clock Distribution Networks (Kluwer Academic Publishers, Norwell, 1997). ISBN # 0-7923-9967-6
R. Gupta, B. Tutuianu, L.T. Pileggi, The Elmore delay as a bound for RC trees with generalized input signals. IEEE Trans. Comput. Aided Des. 16(1), 95–104 (1997)
N.J. Higham, The scaling and squaring method for the matrix exponential revisited. SIAM Rev. 51, 747–764 (2009)
Y.I. Ismail, E.G. Friedman, J.L. Neves, Equivalent Elmore delay for RLC trees. IEEE Trans. Comput. Aided Des. 19(1), 83–97 (2000)
Y.I. Ismail, E.G. Friedman, Fast and accurate simulation of tree structured interconnect, in Proceedings of the 43rd IEEE circuits and systems Mid-west Symposium (2000), pp. 1130–1134
Y.I. Ismail, E.G. Friedman, Effects of inductance on the propagation delay and repeater insertion in VLSI circuits. IEEE Trans. VLSI 8(2), 195–206 (2000)
X. Ji, L. Ge, Z. Wang, Analysis of on-chip distributed interconnects based on Pade expansion. J. Control Theory Appl. 7(1), 92–96 (2009)
A.B. Kahng, S. Muddu, An analytical delay model for RLC interconnects. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 16(12), 1507–1514 (1997)
A.B. Kahng, S. Muddu, Two-pole analysis of interconnection trees, in Proceedings of IEEE MCMC Conference (MCMC-95), Santa Cruz, California, USA, (1995), pp. 105–110
X.-C. Li, J.-F. Mao, H.-F. Huang, Accurate analysis of interconnect trees with distributed RLC model and moment matching. IEEE Trans. Microw. Theory Tech. 52(9), 2199–2206 (2004)
C. Li, X. Zhu, C. Gu, Matrix Padé-type method for computing the matrix exponential. Appl. Math. 2, 247–253 (2011)
W.-K. Loo, K.-S. Tan, Y.-K. Teh, A study and design of CMOS H-tree clock distribution network in system-on-chip, in Proceedings of the 8th IEEE international conference on ASIC, Changsha, Hunan, China (2009), pp. 411–414
N. Rakuljic, I. Galton, Tree-structured DEM DACs with arbitrary numbers of levels. IEEE Trans. CAS I 52(2), 313–322 (2010)
B. Ravelo, A.K. Jastrzebski, Modelling of symmetrical distributed clock RC H-tree, in Proceedings of IEEE international symposium on electromagnetic compatibility (EMC EUROPE) (2012), pp. 1–6
J. Rosenfeld, E.G. Friedman, Design methodology for global resonant H-tree clock distribution networks. IEEE Trans. VLSI Syst. 15(2), 135–148 (2007)
S. Roy, A. Dounavis, Closed-form delay and crosstalk models for RLC on-chip interconnects using a matrix rational approximation. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 28(10), 1481–1492 (2009)
J. Rubinstein, P. Penfield Jr, M.A. Horowitz, Signal delay in RC tree networks. IEEE Trans. Comput. Aided Des. 2(3), 202–211 (1983)
T. Sakurai, Closed-form expressions for interconnection delay, coupling, and crosstalk in VLSI’s. IEEE Trans. Electron Devices 40(1), 118–124 (1993)
Semiconductor Industry Association, The International Technology Roadmap for Semiconductors (1999)
K.T. Tang, E.G. Friedman, Delay and power expressions characterizing a CMOS inverter driving an RLC load, in Proceedings of the IEEE international symposium on circuits and systems (2000), pp. III.283–III.286
C.-W.A. Tsao, C.-K. Koh, A clock tree router for general skew constraints. J. ACM Trans. Des. Autom. Electron. Syst. 7(3), 359–379 (2002)
K. Yamakoshi, M. Ino, Generalized Elmore delay expression for distributed RC tree networks. Electron. Lett. 29(7), 617–618 (1993)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Kavicharan, M., Murthy, N.S., Rao, N.B. et al. Modeling and Analysis of On-Chip Single and H-tree Distributed RLC Interconnects. Circuits Syst Signal Process 35, 3049–3065 (2016). https://doi.org/10.1007/s00034-015-0188-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00034-015-0188-0