Abstract
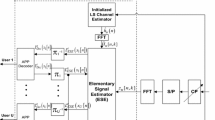
This paper presents adaptive channel prediction techniques for wireless orthogonal frequency division multiplexing (OFDM) systems using cyclic prefix (CP). The CP not only combats intersymbol interference, but also precludes requirement of additional training symbols. The proposed adaptive algorithms exploit the channel state information contained in CP of received OFDM symbol, under the time-invariant and time-variant wireless multipath Rayleigh fading channels. For channel prediction, the convergence and tracking characteristics of conventional recursive least squares (RLS) algorithm, numeric variable forgetting factor RLS (NVFF-RLS) algorithm, Kalman filtering (KF) algorithm and reduced Kalman least mean squares (RK-LMS) algorithm are compared. The simulation results are presented to demonstrate that KF algorithm is the best available technique as compared to RK-LMS, RLS and NVFF-RLS algorithms by providing low mean square channel prediction error. But RK-LMS and NVFF-RLS algorithms exhibit lower computational complexity than KF algorithm. Under typical conditions, the tracking performance of RK-LMS is comparable to RLS algorithm. However, RK-LMS algorithm fails to perform well in convergence mode. For time-variant multipath fading channel prediction, the presented NVFF-RLS algorithm supersedes RLS algorithm in the channel tracking mode under moderately high fade rate conditions. However, under appropriate parameter setting in \(2\times 1\) space–time block-coded OFDM system, NVFF-RLS algorithm bestows enhanced channel tracking performance than RLS algorithm under static as well as dynamic environment, which leads to significant reduction in symbol error rate.












Similar content being viewed by others
References
D. Agarwal, V. Tarokh, A. Naguib, N. Seshadri, Space–time coded OFDM for high data rate wireless communication over wideband channels, in Proceedings of 48th IEEE Vehicular Technology Conference, vol. 3 (Ottawa, 1998), pp. 2232–2236
S.M. Alamouti, A simple transmit diversity technique for wireless communications. IEEE J. Sel. Areas Commun. 16(8), 1451–1458 (1998)
H. Ali, A cyclic prefix based adaptive channel estimation algorithm for multicarrier systems, in Proceedings of IEEE International Symposium on Signal Processing and Information Technology (ISSPIT) (Luxor, 2010), pp. 215–218
J.A.C. Bingham, Multicarrier modulation for data transmission: an idea whose time has come. IEEE Commun. Mag. 28(5), 5–14 (1990)
L. Chen, B. Chen, A robust adaptive DFE receiver for DS-CDMA system under multipath fading channels. IEEE Trans. Signal Process. 49(7), 1523–1532 (2001)
Q. Cheng, Residue carrier frequency offset estimation using cyclic prefix in OFDM systems, in Proceedings of TENCON-2009 IEEE Region 10 Conference (Singapore, 2009), pp. 1–5
Y.S. Cho, S.B. Kim, E.J. Powers, Time-frequency analysis using AR models with variable forgetting factors, in Proceedings of ICASSP’90 (Albuquerque, 1990), pp. 2479–2482
Y.S. Cho, S.B. Kim, E.J. Powers, Time-varying spectral estimation using AR models with variable forgetting factor. IEEE Trans. Signal Process. 39(6), 1422–1426 (1991)
J.S. Chow, J.C. Tu, J.M. Cioffi, A discrete multitone transceiver system for HDSL application. IEEE J. Sel. Areas Commun. 9(6), 895–908 (1991)
J. Coon, M. Beach, J. McGeehan, Optimal training sequences for channel estimation in cyclic-prefix-based single-carrier systems with transmit diversity. IEEE Signal Process. Lett. 11(9), 729–732 (2004)
L. Davis, I. Collings, R. Evans, Coupled estimators for equalization of fast-fading mobile channels. IEEE Trans. Commun. 46(10), 1262–1265 (1998)
M. Engels, Wireless OFDM Systems: How to Make Them Work? (Kluwer, Boston, 2002)
S. Gazor, Predictions in LMS-Type adaptive algorithms for smoothly time-varying environments. IEEE Trans. Signal Process. 47(6), 1735–1739 (1999)
M.S. Grewal, A.P. Andrew, Kalman Filtering: Theory and Practice (Prentice-Hall, Englewood Cliffs, 1993)
A. Grover, A.K. Kohli, Space–time block-coded systems using numeric variable forgetting factor least squares channel estimator. Int. J. Phys. Sci. 6(32), 7361–7370 (2011)
A. Grover, D.S. Kapoor, A.K. Kohli, Characterisation of impulse noise effects on space–time block-coded orthogonal frequency division multiplexing (OFDM) signal reception. Int. J. Phys. Sci. 7(25), 4003–4011 (2012)
G.H. Golub, Matrix Computations (The Johan Hopkins University Press, Baltimore, 1989)
P. Gupta, D.K. Mehra, A novel technique for channel estimation and equalization for high mobility OFDM systems. Wirel. Pers. Commun. 49(4), 613–631 (2009)
L. Hanzo, T. Keller, M. Muenster, B.J. Choi, OFDM and MC-CDMA for Broadband Multi-User Communications, WLANs and Broadcasting (Wiley, New York, 2003)
S. Haykin, Adaptive Filter Theory, 4th edn. (Pearson Education, New York, 2002)
P. Hoeher, S. Kaiser, P. Robertson, Two-dimensional pilot-symbol aided channel estimation by Wiener filtering, in Proceedings of International Conference on Acoustics, Speech and Signal Processing: IEEE (Munich, Germany, 1997), pp. 1845–1848
W.C. Jakes, Microwave Mobile Communications (McGraw-Hill, New York, 1994)
T. Kim, I. Eo, Reliable blind channel estimation scheme based on cross-correlated cyclic prefix for OFDM system, in Proceedings of The 8th International Conference on Advanced Communication Technology, ICACT: IEEE (Phoenix Park, 2006), pp. 3–5
A.K. Kohli, D.K. Mehra, Tracking of time-varying channels using two-step LMS-type adaptive algorithm. IEEE Trans. Signal Process. 54(7), 2606–2615 (2006)
A.K. Kohli, D.K. Mehra, Adaptive multiuser channel estimator using reduced Kalman/LMS algorithm. Wirel. Pers. Commun. 46(4), 507–521 (2008)
A.K. Kohli, D.K. Mehra, Adaptive DFE multiuser receiver for CDMA systems using two-step LMS-type algorithm: an equalization approach. Wirel. Pers. Commun. 54(3), 543–558 (2010)
A.K. Kohli, A. Rai, M.K. Patel, Variable forgetting factor LS algorithm for polynomial channel model. ISRN Signal Processing. ID: 915259, 1–4 (2011)
A.K. Kohli, Fading model for antenna array receiver for a ring-type cluster of scatterers. Int. J. Electron. 98(7), 933–940 (2011)
A.K. Kohli, A. Rai, Numeric variable forgetting factor RLS algorithm for second-order Volterra filtering. Circuits Syst. Signal Process. 32(1), 223–232 (2013)
A.P. Liavas, P.A. Regalia, On the numerical stability and accuracy of the conventional recursive least squares algorithm. IEEE Trans. Signal Process. 47(1), 88–96 (1999)
P. Ling, W.G. Lim, H. Ali, Adaptive channel estimation using least mean squares algorithm for cyclic prefix OFDM systems, in Proceedings of IEEE 9th Malaysia International Conference on Communications (MICC) (Kuala Lumpur, 2009), pp. 789–793
Z. Liu, X. Ma, G.B. Giannakis, Space–time coding and Kalman filtering for time-selective fading channels. IEEE Trans. Commun. 50(2), 183–186 (2002)
S. Lu, B. Narasimhan, N. Al-Dhahir, A novel SFBC-OFDM scheme for doubly selective channels. IEEE Trans. Veh. Technol. 58(5), 2573–2578 (2009)
X. Ma, G.B. Giannakis, Maximum-diversity transmissions over doubly selective wireless channels. IEEE Trans. Inf. Theory 49(7), 1832–1840 (2003)
M.D. Nisar, H. Nottensteiner, W. Utschick, T. Hindelang, On channel estimation and equalization of OFDM systems with insufficient cyclic prefix, in Proceedings of IEEE 65th Vehicular Technology Conference (Dublin, 2007), pp. 1445–1449
A. Papoulis, Probability, Random Variables, and Stochastic Processes, 3rd edn. (McGraw-Hill, New York, 1991)
J.G. Proakis, Digital Communications, 3rd edn. (McGraw-Hill, New York, 1995)
A.A. Quadeer, M.S. Sohail, Enhanced channel estimation using cyclic prefix in MIMO STBC OFDM systems, in Proceedings of IEEE International Symposium on Signal Processing and Information Technology (ISSPIT) (Luxor, 2010), pp. 277–282
A.H. Sayed, T. Kailath, A state-space approach to adaptive RLS filtering. IEEE Trans. Signal Process. Mag. 11(3), 18–60 (1994)
H. Senol, E. Panayirci, H.V. Poor, Nondata-aided joint channel estimation and equalization for OFDM systems in very rapidly varying mobile channels. IEEE Trans. Signal Process. 60(8), 4236–4253 (2012)
S. Singh, A.K. Kohli, Wireless fading paradigm for antenna array receiver for a disk-type cluster of scatterers. Circuits Syst. Signal Process. 33(4), 1231–1244 (2014)
S. Song, J.S. Lim, S.J. Baek, K.M. Sung, Variable forgetting factor linear least squares algorithm for frequency selective fading channel estimation. IEEE Trans. Veh. Technol. 51(3), 613–616 (2002)
P. Sudheesh, A. Jayakumar, Cyclic prefix assisted sparse channel estimation for OFDM systems, in Proceedings of International Conference on Computing, Communication and Applications: IEEE (Tamilnadu, 2012), pp. 1–4
M. Uysal, N. Al-Dhahir, C.N. Georghiades, A space–time block-coded OFDM scheme for unknown frequency-selective fading channels. IEEE Commun. Lett. 5(10), 393–395 (2001)
A. Visakh, N. Upadhyay, Channel estimation for OFDM systems using Kalman filter algorithm, in Proceedings of the 1st International Conference on Wireless Technologies for Humanitarian Relief: ACM (2011), pp. 49–52
H.S. Wang, P. Chang, On verifying the first-order Markovian assumption for a Rayleigh fading channel model. IEEE Trans. Veh. Technol. 45(2), 353–357 (1996)
X. Wang, K.J.R. Liu, Adaptive channel estimation using cyclic prefix in multicarrier modulation system. IEEE Commun. Lett. 3(10), 291–293 (1999)
X. Wang, K.J.R. Liu, Performance analysis for adaptive channel estimation exploiting cyclic prefix in multicarrier modulation systems. IEEE Trans. Commun. 51(1), 94–105 (2003)
B. Widrow, J.M. McCool, M.G. Larimore, C.R. Johnson, Stationary and nonstationary learning characteristics of the LMS adaptive filter. Proc. IEEE 64(8), 1151–1162 (1996)
R.A. Ziegler, J.M. Cioffi, Estimation of time-varying digital radio channel. IEEE Trans. Veh. Technol. 41(2), 134–151 (1992)
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
1.1 Brief Description of \({2\times 1}\) STBC-OFDM System Model
Let us consider \(2\times 1\) STBC-OFDM system with two transmitters (TX1 and TX2) and one receiver (RX1) antennas (as in [44]), in which the kth and \((k+1)\)th OFDM symbol blocks are denoted as \({\vec {\mathbf{X }}}_{\mathbf{o }} =\left[ {{\begin{array}{cccc} {X_{0,k} }&{}\; {X_{1,k} }&{}\; \ldots &{}\; {X_{N-1,k} } \\ \end{array} }} \right] _{N\times 1}^T \) and \({\vec {\mathbf{X }}}_{\mathbf{e }} =\left[ {{\begin{array}{cccc} {X_{0,k+1} }&{}\; {X_{1,k+1} }&{}\; \ldots &{}\; {X_{N-1,k+1} } \\ \end{array} }} \right] _{N\times 1}^T \), respectively. By performing IFFT operation, the \({\vec {\mathbf{X }}}_{\mathbf{o }}\) and \({\vec {\mathbf{X }}}_{\mathbf{e }} \) can be expressed in time domain as \({\vec {\mathbf{x }}}_{\mathbf{o }} =\left[ {{\begin{array}{cccc} {x_{0,k} }&{}\; {x_{1,k} }&{}\; \ldots &{}\; {x_{N-1,k} } \\ \end{array} }} \right] _{N\times 1}^T \) and \({\vec {\mathbf{x }}}_{\mathbf{e }} =\left[ {{\begin{array}{cccc} {x_{0,k+1} }&{}\; {x_{1,k+1} }&{}\; \ldots &{}\; {x_{N-1,k+1} } \\ \end{array} }} \right] _{N\times 1}^T \), respectively. Subsequently by incorporating CP, these two OFDM symbol blocks are represented as
Applying the space–time block-coding scheme using these two OFDM symbol blocks with CP [44], it can be shown that
The transmitted wireless OFDM signals encounter multipath fading with L channel tap coefficients, which leads to \(G\ge 2L-2\) in the present scenario. The two independent wireless channel tap coefficient vectors are \({\vec {\mathbf{h }}}_{{\mathbf{1,k }}} \) (from TX1 to RX1) and \({\vec {\mathbf{h }}}_{{\mathbf{2,k }}} \) (from TX2 to RX1), respectively. The wireless channel tap coefficient vectors are assumed to be constant for two OFDM symbol blocks, such that
The received composite wireless signals at the receiver are
The cyclic prefix part is extracted at the receiver considering \(G=2L-2\) (as in Sect. 2.2) to provide
where
In matrix form, (49) and (50) can be rearranged by invoking (47) to give
where
Analogous to (19), if the channel is assumed to be constant for two consecutive OFDM symbol blocks, then
where \({\vec {\mathbf{A }}}_{\mathbf{2 }} =\alpha {\vec {\mathbf{I }}}_{2L\times 2L} \) is the channel state transition matrix with \(2L\times 2L\) dimensional identity matrix \({\vec {\mathbf{I }}}\). Using the aforementioned Eq. (53), the presented channel estimation schemes are used to obtain \({\hat{{\mathbf{h }}}}_{\mathbf{1,k }} =\hat{{{\mathbf{h }}}}_{{\mathbf{1,k }}+1} \) and \({\hat{\mathbf{h }}}_{{\mathbf{2,k }}} =\hat{{{\mathbf{h }}}}_{{\mathbf{2,k+1 }}} \). Further, this estimated/predicted channel state information is used to decode the STBC-OFDM symbols, as in [1, 2, 44].
Rights and permissions
About this article
Cite this article
Kohli, A.K., Kapoor, D.S. Adaptive Filtering Techniques using Cyclic Prefix in OFDM Systems for Multipath Fading Channel Prediction. Circuits Syst Signal Process 35, 3595–3618 (2016). https://doi.org/10.1007/s00034-015-0214-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00034-015-0214-2