Digital Background Calibration of Residue Amplifier Non-idealities in Pipelined ADCs

Abstract

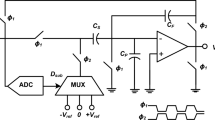
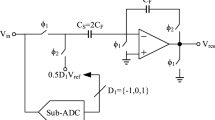
In this paper, a digital background calibration technique for pipelined analog-to-digital converters (ADCs) is presented to continuously mitigate the conversion errors arising from the residue amplifier imperfections. The introduced method indirectly measures the digitized residue errors based on a novel principle. In the proposed method, the digitized residue errors are measured through the probability distribution of the digitized residue and a two-level pseudorandom noise sequence. Behavioral simulations are provided for a 12-bit pipelined ADC architecture to show the effectiveness of the proposed technique. The simulation results show that the signal-to-noise and distortion ratio is improved from 42.94 to 72.85 dB using the presented calibration technique. The required number of samples for convergence is approximately 5 $\times$ $10^{6}$ clock cycles.

Appendices

Appendix 1

In this appendix, the transformation of a shifted CDF through the function $g_{\mathrm{ad1}}(.)=g_{\mathrm{d1}}(g_{\mathrm{a1}}(.))$ is described. The relation between the input and output PDFs of the function $g_{\mathrm{ad1}}(.)$ is given by

$$\begin{aligned} p_{DR1} \left( {D_\mathrm{r1}} \right) =p_{VR1} \left( {V_\mathrm{r1} } \right) \left| {\frac{dg_{ad1} \left( {V_\mathrm{r1} } \right) }{\hbox {d}V_\mathrm{r1}}} \right| _{V_\mathrm{r1} =g_{ad1} ^{-1}\left( {D_\mathrm{r1} } \right) }^{-1} \end{aligned}$$

(45)

where $p_{\mathrm{DR1}}(.)$ represents the digitized residue PDF and $p_{\mathrm{VR1}}(.)$ stands for the residue voltage PDF. Since $g_{\mathrm{ad1}}(.)$ is often weakly nonlinear, hence the following approximations can be used

$$\begin{aligned}&\left| {\frac{dg_{ad1} \left( {V_\mathrm{r1} } \right) }{\hbox {d}V_\mathrm{r1} }} \right| ^{-1}\approx \left( {1-e_1 } \right) -e_2 V_\mathrm{r1} -e_3 V_\mathrm{r1}^{2}, \end{aligned}$$

(46)

$$\begin{aligned}&\quad V_\mathrm{r1} = g_{ad1}^{-1} \left( {D_\mathrm{r1} } \right) , \end{aligned}$$

(47)

to simplify the analysis. Using the above approximations, the CDF of $D_{\mathrm{r1}}$ and $V_{\mathrm{r1}}$ is given by

$$\begin{aligned} P\left( {D_\mathrm{r1} } \right)= & {} \int \limits _{-\Delta /2}^{g_{ad1} ^{-1}\left( {D_\mathrm{r1} } \right) } {p_{VR1} \left( {V_\mathrm{r1} } \right) \left( {1-e_1 -e_2 V_\mathrm{r1} -e_3 V_\mathrm{r1} ^{2}} \right) \hbox {d}V_\mathrm{r1}}, \end{aligned}$$

(48)

$$\begin{aligned} P_{VR1} \left( {D_\mathrm{r1} } \right)= & {} \int \limits _{-\Delta /2}^{g_{ad1} ^{-1}\left( {D_\mathrm{r1} } \right) } {p_{VR1} \left( {V_\mathrm{r1} } \right) \hbox {d}V_\mathrm{r1}}. \end{aligned}$$

(49)

Applying the assumption that $p_{\mathrm{VR1}}(.)$ is uniformly distributed within the interval [$-\Delta /2,\, \Delta /2$] at a value of $1/\Delta$, the CDFs in (48) and (49) can be represented as follows

$$\begin{aligned} P\left( {D_\mathrm{r1} } \right)= & {} \frac{1}{\Delta }\left\{ {\begin{array}{l} \left( {1-e_1 } \right) g_{ad1}^{-1} \left( {D_\mathrm{r1} } \right) -\frac{e_2 }{2}g_{ad1}^{-1} \left( {D_\mathrm{r1} } \right) ^{2} \\ -\frac{e_3 }{3}g_{ad1}^{-1} \left( {D_\mathrm{r1} } \right) ^{3} \\ \end{array}} \right\} -\eta , \end{aligned}$$

(50)

$$\begin{aligned} P_{VR1} \left( {D_\mathrm{r1} } \right)= & {} \frac{g_{ad1}^{-1} \left( {D_\mathrm{r1} } \right) }{\Delta }-\eta _{vr1} \end{aligned}$$

(51)

where $\eta = \{-(1-e_{1}) -- e_{2}/2 + e_{3}/3\}/2$ and $\eta _{\mathrm{vr1}} = -1/2$. If the constants $\eta$ and $\eta _{\mathrm{o1}}$ are omitted from (50) and (51), then $P(D_{\mathrm{r1}})$ can simply be expressed as a function of $P_{\mathrm{VR1}}(D_{\mathrm{r1}})$. For this reason, the shifted CDF of $D_{\mathrm{r1}}$ and $V_{\mathrm{r1}}$ are defined as $H(D_{\mathrm{r1}})=P(D_{\mathrm{r1}}) +\eta$ and $H_{\mathrm{VR1}}(D_{\mathrm{r1}})=P_{\mathrm{VR1}}(D_{\mathrm{r1}}) +\eta _{\mathrm{vr1}}$, respectively. Therefore, $g_{\mathrm{ad1}}^{-1}(D_{\mathrm{r1}})$ can be written as a function of $H_{\mathrm{VR1}}(D_{\mathrm{r1}})$ as

$$\begin{aligned} g_{ad1}^{-1} \left( {D_\mathrm{r1} } \right) =\Delta H_{VR1} \left( {D_\mathrm{r1} } \right) . \end{aligned}$$

(52)

Besides, the shifted CDF $H(D_{\mathrm{r1}})$ can be expressed as follows

$$\begin{aligned} H\left( {D_\mathrm{r1}} \right) \approx \left( {1-e_1 } \right) H_{VR1} \left( {D_\mathrm{r1}} \right) -e_2 \frac{\Delta }{2}H_{VR1} \left( {D_\mathrm{r1} } \right) ^{2}-e_3 \frac{\Delta ^{3}}{3}H_{VR1} \left( {D_\mathrm{r1} } \right) ^{3}.\qquad \end{aligned}$$

(53)

From the basic probability, the shifted CDF H(.) on condition PN can also be represented by

$$\begin{aligned} H_{+1} \left( {D_\mathrm{r1} } \right)\approx & {} \left( {1-e_1 } \right) H_{VR1,+1} \left( {D_\mathrm{r1} } \right) -e_2 \frac{\Delta ^{2}}{2}H_{VR1,+1} \left( {D_\mathrm{r1} } \right) ^{2} \nonumber \\&-e_3 \frac{\Delta ^{3}}{3}H_{VR1,+1} \left( {D_\mathrm{r1} } \right) ^{3}, \end{aligned}$$

(54)

$$\begin{aligned} H_{-1} \left( {D_\mathrm{r1} } \right)\approx & {} \left( {1-e_1} \right) H_{VR1,-1} \left( {D_\mathrm{r1} } \right) \nonumber \\&-e_2 \frac{\Delta ^{2}}{2}H_{VR1,-1} \left( {D_\mathrm{r1} } \right) ^{2}-e_3 \frac{\Delta ^{3}}{3}H_{VR1,-1} \left( {D_\mathrm{r1} } \right) ^{3} \end{aligned}$$

(55)

where $H_{\mathrm{VR1},+1}(.)$ and $H_{\mathrm{VR1},-1}(.)$ are the shifted CCDFs of the residue voltage for the states PN = +1 and PN = -1, correspondingly. Plugging (54) and (55) into (20), the distribution error can be expressed as

$$\begin{aligned} e_{dis} \left( {D_\mathrm{r1} } \right) \approx \left( {1-e_1 } \right) EE_1 \left( {D_\mathrm{r1} } \right) -e_2 \frac{\Delta ^{2}}{2}EE_2 \left( {D_\mathrm{r1} } \right) -e_3 \frac{\Delta ^{2}}{3}EE_3 \left( {D_\mathrm{r1}} \right) \end{aligned}$$

(56)

where $EE_{1}$(.), $EE_{2}$(.), and $EE_{3}$(.) denote the estimated errors, given by

$$\begin{aligned} \textit{EE}_m \left( {D_\mathrm{r1} } \right) =H_{VR1,+1} \left( {D_\mathrm{r1}} \right) ^{m}-H_{VR1,-1} \left( {D_\mathrm{r1}} \right) ^{m} \quad {m=1,2,3} \end{aligned}$$

(57)

Appendix 2

Figure 16 shows the relation between $Mean_{3}$ and $Mean_{1}$ as functions of $e_{1}$ inside the interval $-1/8 < e_{1} < 1/8$ with $N = 128,\, \Delta = 1/8,\, \eta = -0.5$, and $e_{2}=e_{3} = 0$. As seen from the figure, the variation of $Mean_{3}$ is approximately identical to 0.2 times the variation of $Mean_{1}$ (i.e., $Mean_{3} = 0.2\cdot Mean_{1})$. Consequently, the impact of $e_{1}$ on $Mean_{3}$ can be considered as an offset error. For this reason, the difference $Mean_{3} - 0.2\cdot Mean_{1}$ is not dependent on the error $e_{1}$ and only proportional to $e_{3}$. Furthermore, $MEE_{3}(.)$ can be modified as $(H_{+1}(.)^{3}-H_{-1}(.)^{3}) - 0.2\cdot MEE_{1}(.)$ in order to mitigate the effect of $e_{1}$ on $MEE_{3}(.)$ (or a simple comparison technique can be employed to detect the condition $e_{1} \approx 0$ in order to alleviate the above-mentioned effect and the third-order calibration can be performed when $e_{1} \approx 0$).

Fig. 16

Ratio of $Mean_{1}$ and $Mean_{3}$ as a function of $e_{1}$

Appendix 3

As discussed earlier, the adaptive machine directly operates on the shifted CCDFs $H_{+1}(.)$ and $H_{-1}(.)$ to measure and remove the digitized residue errors. In addition, $H_{+1}(.)$ and $H_{-1}(.)$ are derived with the assumption that the value of $\eta$ is known. In practice, the value of $\eta$ is not known since it depends on the residue amplifier non-idealities. Consequently, the value of $\eta$ must be estimated. As detailed in Sect. 3.2, since the integrators in (30) force the means $Mean_{1},\, Mean_{2}$, and $Mean_{3}$ to zero, hence these means need to be proportional to the terms $e_{1},\, e_{2}$, and $e_{3}$, correspondingly, and pass through zero when $e_{1},\, e_{2}$, and $e_{3}$ are identical to zero, respectively. However, it will be verified that $Mean_{2}$ and $Mean_{3}$ also depend on the value of $\eta$. In turn, the value of $\eta$ must be adjusted such that $Mean_{\mathrm{m}} \, (m = 1, 2,\, \hbox {and } 3)$ passes through zero at $e_{\mathrm{m}} = 0$.

In the following analysis, the impact of $\eta$ on $Mean_{\mathrm{m}}^{2}$ ($m = 1, 2,\hbox { and } 3)$ is analyzed. Accordingly, in the absence of the digitized residue errors, the minimum value of $Mean_{\mathrm{m}}( \eta )^{2}$ (m = 1, 2, and 3) indicates $Mean_{\mathrm{m}}(\eta ) = 0$. In order to obtain the minimum values of $Mean_{1}^{2},\, Mean_{2}^{2}$, and $Mean_{3}^{2}$ with respect to $\eta$, the first derivative of $Mean_{1}^{2},\, Mean_{2}^{2}$, and $Mean_{3}^{2}$ with respect to $\eta$ is required. Plugging (21) and (22) into (28), and substituting (28) into (27), it is clear to verify that the first derivative of $Mean_{1}^{2}$ with respect to $\eta$ is equal to zero; hence $Mean_{1}^{2}$ is independent from $\eta$. In addition, the first derivatives of $Mean_{2}^{2}$ and $Mean_{3}^{2}$ with respect to $\eta$ are identical to $4\cdot Mean_{2}\cdot Mean_{1}$ and $6\cdot Mean_{3}\cdot Mean_{2}$, respectively. Therefore, in the absence of the digitized residue errors, $Mean_{2}^{2}$ and $Mean_{3}^{2}$ are minimized as long as $Mean_{2}(\eta ) = 0$. Plugging (21) and (22) into (28), and substituting (28) into (27) for $m = 2$, it can be proved that $Mean_{2}$ is identical to zero provided that $\eta$ is equal to

$$\begin{aligned} \eta =\frac{\sum \nolimits _{s=0}^N {P_{-1} \left( {Ts+\Delta } \right) ^{2}-P_{+1} \left( {Ts} \right) ^{2}} }{2\sum \nolimits _{s=0}^N {P_{+1} \left( {Ts} \right) -P_{-1} \left( {Ts+\Delta } \right) } } \end{aligned}$$

(58)

where $T = -\Delta /N$. For a uniformly distributed residue voltage, with $N = 128$ and $e_{2}= e_{3} = 0$, and different values of $e_{1},\, \eta$ is obtained approximately identical to $-$0.5.

Fig. 17

$Mean_{1}^{2},\, Mean_{2}^{2}$, and $Mean_{3}^{2}$ versus $\eta$

Figure 17 shows $Mean_{1}^{2},\, Mean_{2}^{2}$, and $Mean_{3}^{2}$ as functions of $\eta$ with $e_{1} = -0.6/8,\, e_{2}=e_{3} = 0,\, \Delta = 1/8$, and $N = 128$. Because $e_{2}$ and $e_{3}$ are set to zero, it is expected that $Mean_{2}^{2}$ and $Mean_{3}^{2}$ must be identical to zero. As depicted in Fig. 17, $Mean_{1}^{2}$ is independent of $\eta$, while $Mean_{2}^{2}$ and $Mean_{3}^{2}$ vary with $\eta$, and these means are also minimized for $\eta = -0.5$. Accordingly, $Mean_{\mathrm{m}}$ (m = 2 and 3) becomes equal to zero for $\eta = -0.5$. In this design, $\eta = -0.5$ is exploited and the described technique works well with this choice, as validated in Sect. 4 with different input signals.