Skip to main content
Springer Nature Link
Log in

Synthetic Aperture Radar Imaging Using Basis Selection Compressed Sensing

  • Published:
Circuits, Systems, and Signal Processing Aims and scope Submit manuscript

Abstract

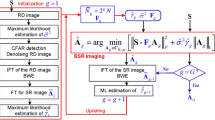
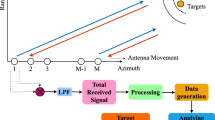
A compressed sensing method with basis selection is applied to a millimeter-wave synthetic aperture radar (SAR) imaging system. With a large candidate set of bases to choose from and without any a priori knowledge of the proper basis, the proposed method selects the sparsifying basis during the first few iterations of the L1 optimization according to the information from incomplete measurements and the coherence between the measurement matrix and sparsifying matrices. Several decision metrics can be used to select the basis, including the impulsiveness and Gini index of the available image at the current iteration. The proposed method is tested on two examples: a simulated image and its SAR measurement, and an experimental measurement obtained at 150 GHz via roaster scanning. The results from the simulation and experiment indicate that the proposed algorithm can always find a very good basis from the set of over 270 bases within the first two to five iterations of the L1 optimization.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

We’re sorry, something doesn't seem to be working properly.

Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. M. Aharon, M. Elad, A. Bruckstein, K-SVD: an algorithm for designing overcomplete dictionaries for sparse representation. IEEE Trans. Signal Proc. 54, 4311–4322 (2006). doi:10.1109/TSP.2006.881199

    Article  Google Scholar 

  2. C.M. Akujuobi, O.O. Odejide, A. Annamalai, G.L. Fudge, Sparseness measures of signals for compressive sampling, in IEEE International Symposium on Signal Processing and Information Technology (2007), pp. 1042–1047. doi:10.1109/ISSPIT.2007.4458145

  3. C.D. Austin, E. Ertin, R.L. Moses, Sparse signal methods for 3-D radar imaging. IEEE J. Sel. Top. Signal Process. 5, 408–423 (2011). doi:10.1109/JSTSP.2010.2090128

    Article  Google Scholar 

  4. E.J. Candes, J. Romberg, T. Tao, Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 52, 489–509 (2006). doi:10.1109/TIT.2005.862083

    Article  MathSciNet  MATH  Google Scholar 

  5. E.J. Candes, M.B. Wakin, An introduction to compressive sampling. IEEE Signal Process. Mag. 25, 21–30 (2008). doi:10.1109/MSP.2007.914731

    Article  Google Scholar 

  6. J.T. Case, S. Kharkovsky, R. Zoughi, G. Steffes, F.L. Hepburn, Millimeter wave holographical inspection of honeycomb composites. 975, 970–975 (2008). doi:10.1063/1.2902771

  7. H.W. Chen, L.W. Kang, C.S. Lu, Dictionary learning-based distributed compressive video sensing, in Picture Coding Symposium (PCS) (2010), pp. 210–213. doi:10.1109/PCS.2010.5702466

  8. I. Daubechies, Ten Lectures on Wavelets (SIAM, PA, 1992). doi:10.1137/1.9781611970104

  9. D.L. Donoho, Compressed sensing. IEEE Trans. Inf. Theory 52, 1289–1306 (2006). doi:10.1109/TIT.2006.871582

    Article  MathSciNet  MATH  Google Scholar 

  10. J.M. Duarte-Carvajalino, G. Sapiro, Learning to sense sparse signals: simultaneous sensing matrix and sparsifying dictionary optimization. IEEE Trans. Image Process. 18, 1395–1408 (2009). doi:10.1109/TIP.2009.2022459

    Article  MathSciNet  Google Scholar 

  11. H. Kajbaf, J.T. Case, Y.R. Zheng, S. Kharkovsky, R. Zoughi, Quantitative and qualitative comparison of SAR images from incomplete measurements using compressed sensing and nonuniform FFT, in IEEE Radar Conference (Radar’11) (2011), pp. 592–596

  12. H. Kajbaf, Compressed sensing for 3D microwave imaging system. Ph. D. dissertation, Missouri University of Science and Technology, Chapter 3 (2012). doi:10.1109/RADAR.2011.5960606

  13. H. Kajbaf, J.T. Case, Z. Yang, Y.R. Zheng, Compressed sensing for SAR-based wideband 3D microwave imaging system using nonuniform FFT. IET Radar Sonar Navig. (2013). doi:10.1049/iet-rsn.2012.0149

  14. S. Kharkovsky, R. Zoughi, Microwave and millimeter wave nondestructive testing and evaluation: overview and recent advances. IEEE Instrum. Meas. Mag. 10, 26–38 (2007). doi:10.1109/MIM.2007.364985

    Article  Google Scholar 

  15. T. Goldstein, S. Osher, The split Bregman algorithm for L1 regularized problems. UCLA CAM Report (2008), pp. 08–29. doi:10.1137/080725891

  16. N. Hurley, S. Rickard, Comparing measures of sparsity, in IEEE Workshop on Machine Learning for Signal Processing (2008), pp. 4723–4741. doi:10.1109/MLSP.2008.4685455

  17. M. Lustig, D.L. Donoho, J.M. Pauly, Sparse MRI: the application of compressed sensing for rapid MR imaging. Magn. Reson. Med. 58, 1182–1195 (2007). doi:10.1002/mrm.21391

    Article  Google Scholar 

  18. G. Peyré, Best basis compressed sensing. IEEE Trans. Signal Process. 58, 2613–2622 (2010). doi:10.1109/TSP.2010.2042490

    Article  MathSciNet  Google Scholar 

  19. L.C. Potter, E. Ertin, J.T. Parker, M. Cetin, Sparsity and compressed sensing in radar imaging. Proc. IEEE 98, 1006–1020 (2010). doi:10.1109/JPROC.2009.2037526

    Article  Google Scholar 

  20. P. Purkait, B. Chanda, Super resolution image reconstruction through Bregman iteration using morphologic regularization. IEEE Trans. Image Process. 21, 4029–4039 (2012). doi:10.1109/TIP.2012.2201492

    Article  MathSciNet  Google Scholar 

  21. S. Ravishankar, Y. Bresler, MR image reconstruction from highly undersampled k-space data by dictionary learning. IEEE Trans. Med. Imaging 30, 1028–1041 (2011). doi:10.1109/TMI.2010.2090538

    Article  Google Scholar 

  22. T.A. Schonhoff, A.A. Giordano, Detection and Estimation Theory and Its Applications (Prentice Hall, Englewood Cliffs, 2006)

    Google Scholar 

  23. A. Soni, J. Haupt, Efficient adaptive compressive sensing using sparse hierarchical learned dictionaries, in 2011 Conference Record of the Forty Fifth Asilomar Conference on Signals, Systems and Computers (ASILOMAR) (2011), pp. 1250–1254. doi:10.1109/ACSSC.2011.6190216

  24. M. Soumekh, Bistatic synthetic aperture radar inversion with application in dynamic object imaging. IEEE Trans. Signal Process. 39, 2044–2055 (1991). doi:10.1109/78.134436

    Article  Google Scholar 

  25. Stanford University, WaveLab 850. http://statweb.stanford.edu/~wavelab/. Retrived Feb. 2014

  26. J.J. Thiagarajan, K.N. Ramamurthy, A. Spanias, Multilevel dictionary learning for sparse representation of images, in Digital Signal Processing Workshop and IEEE Signal Processing Education Workshop (DSP/SPE) (2011), pp. 271–276. doi:10.1109/DSP-SPE.2011.5739224

  27. Z. Wang, A.C. Bovik, H.R. Sheikh, E.P. Simoncelli, Image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process. 13, 600–612 (2004). doi:10.1109/TIP.2003.819861

    Article  Google Scholar 

  28. J. Yang, Y. Zhang, Alternating Algorithms for \(\ell _1\)-Problems in Compressive Sensing. Rice University CAAM. http://www.caam.rice.edu/~zhang/reports/tr0937 (2010). doi:10.1137/090777761

  29. Z. Yang, Y.R. Zheng, Near-field 3-D synthetic aperture radar imaging via compressed sensing. IEEE ICASSP 25–30, 2513–2516 (2012). doi:10.1109/ICASSP.2012.6288427

    Google Scholar 

  30. Z. Yang, Y.R. Zheng, A comparative study of compressed sensing approaches for 3-D synthetic aperture radar image reconstruction. Digit. Signal Process. 32, 24–33 (2014). doi:10.1016/j.dsp.2014.05.016

  31. D. Zonoobi, A.A. Kassim, Y.V. Venkatesh, Gini index as sparsity measure for signal reconstruction from compressive samples. IEEE J. Sel. Top. Signal Process. 5, 927–932 (2011). doi:10.1109/JSTSP.2011.2160711

    Article  Google Scholar 

Download references

Acknowledgments

The work of Dongjie Bi and Yongle Xie was supported by the National Natural Science Foundation of China (61371049) and the Specialized Research Fund for the Doctoral Program of High Education of China (20120185110013). The work of Dongjie Bi was performed during his visit at Missouri University of Science and Technology. The work of Yahong Rosa Zheng was supported in part by the Intelligent Systems Center of Missouri University of Science and Technology, the Inter-Discipline Inter-Campus research program of University of Missouri systems, and the Technology Research Institute of Austin. The authors wish to thank Dr. Kristen Donnell of Missouri University of Science and Technology for providing the SAR measurement data in Fig. 6 and Mr. Zengli Yang of Missouri University of Science and Technology for providing the simulation program that generated Fig. 1a.

Author information

Authors and Affiliations

  1. School of Automation Engineering, University of Electronic Science and Technology of China, Chengdu, 611731, People’s Republic of China

    Dongjie Bi & Yongle Xie

  2. Department of Electrical and Computer Engineering, Missouri University of Science and Technology, Rolla, MO, 65409, USA

    Yahong Rosa Zheng

Authors
  1. Dongjie Bi
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Yongle Xie
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Yahong Rosa Zheng
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Dongjie Bi.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bi, D., Xie, Y. & Zheng, Y.R. Synthetic Aperture Radar Imaging Using Basis Selection Compressed Sensing. Circuits Syst Signal Process 34, 2561–2576 (2015). https://doi.org/10.1007/s00034-015-9974-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00034-015-9974-y

Keywords