Skip to main content
Springer Nature Link
Log in

A Variable Step-Size Strategy Based on Error Function for Sparse System Identification

  • Short Paper
  • Published:
Circuits, Systems, and Signal Processing Aims and scope Submit manuscript

Abstract

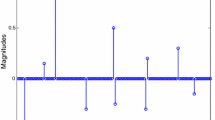
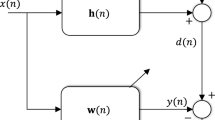
The well-known reweighted zero-attracting least mean square algorithm (RZA-LMS) has been effective for the estimation of sparse system channels. However, the RZA-LMS algorithm utilizes a fixed step size to balance the steady-state mean square error and the convergence speed, resulting in a reduction in its performance. Thus, a trade-off between the convergence rate and the steady-state mean square error must be made. In this paper, utilizing the nonlinear relationship between the step size and the power of the noise-free prior error, a variable step-size strategy based on an error function is proposed. The simulation results indicate that the proposed variable step-size algorithm shows a better performance than the conventional RZA-LMS for both the sparse and the non-sparse systems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. T. Aboulnasr, K. Mayyas, A robust variable step-size LMS-type algorithm: analysis and simulation. IEEE Trans. Signal Process. 45(3), 631–639 (1997)

    Article  Google Scholar 

  2. J. Benesty, S.L. Gay, An improved PNLMS algorithm, in IEEE International Conference on Acoustics, Speech, & Signal Processing (2002), pp. II-1881–II-1884

  3. M.Z.A. Bhotto, A. Antoniou, A family of shrinkage adaptive filtering algorithms. IEEE Trans. Signal Process. 61(7), 1689–1697 (2013)

    Article  MathSciNet  Google Scholar 

  4. Y. Chen, Y. Gu, A.O. Hero, Sparse LMS for system identification, in IEEE International Conference on Acoustics, Speech & Signal Processing (2009), pp. 3125–3128

  5. D.L. Duttweiler, Proportionate normalized least-mean-squares adaptation in echo cancellers. IEEE Trans. Speech Audio Process. 8(5), 508–518 (2000)

    Article  Google Scholar 

  6. H. Deng, M. Doroslovacki, Improving convergence of the PNLMS algorithm for sparse impulse response identification. IEEE Signal Process. Lett. 12(3), 181–184 (2005)

    Article  Google Scholar 

  7. H. Deng, M. Doroslovacki, Proportionate adaptive algorithms for network echo cancellation. IEEE Trans. Signal Process. 54(5), 1794–1803 (2006)

    Article  Google Scholar 

  8. B. Farhang-Boroujeny, Adaptive Filters: Theory and Applications, 2nd edn. (Wiley, Chichester, 2013)

    Book  MATH  Google Scholar 

  9. S.L. Gay, An efficient, fast converging adaptive filter for network echo cancellation, in Conference Record of the Thirty-Second Asilomar Conference on Signals, Systems & Computers (1998), pp. 394–398

  10. Y. Gao, S. Xie, A variable step-size LMS adaptive filtering algorithm and its analysis. Acta Electron. Sin. 29(8), 1094–1097 (2001)

    Google Scholar 

  11. H.C. Huang, J. Lee, A new variable step-size NLMS algorithm and its performance analysis. IEEE Trans. Signal Process. 60(4), 2055–2060 (2012)

    Article  MathSciNet  Google Scholar 

  12. M.A. Iqbal, S.L. Grant, Novel variable step size nlms algorithms for echo cancellation, in IEEE International Conference on Acoustics, Speech and Signal Processing (2008), pp. 241–244

  13. C. Paleologu, J. Benesty, S. Ciochina, Sparse Adaptive Filters for Echo Cancellation (Morgan & Claypool, San Rafael, 2010)

    MATH  Google Scholar 

  14. J. Qin, J. Ouyang, A novel variable step-size LMS adaptive filtering algorithm based on sigmoid function. J. Data Acquis. Process. 12(3), 171–174 (1997)

    Google Scholar 

  15. V. Stojanovic, N. Nedic, Robust Kalman filtering for nonlinear multivariable stochastic systems in the presence of non-Gaussian noise. Int. J. Robust Nonlinear Control 26(3), 445–460 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  16. V. Stojanovic, N. Nedic, Robust identification of OE model with constrained output using optimal input design. J. Frankl. Inst. 353(2), 576–593 (2015)

    Article  MathSciNet  Google Scholar 

  17. Z. Yang, Y.R. Zheng, S.L. Grant, Proportionate affine projection sign algorithms for network echo cancellation. IEEE Trans. Audio Speech Lang. Process. 19(8), 2273–2284 (2011)

    Article  Google Scholar 

Download references

Acknowledgments

This work was supported by Program for ChangJiang Scholars and Innovative Research Team in University (IRT1299), and the special fund of Chongqing Key Laboratory (CSTC).

Author information

Authors and Affiliations

  1. Chongqing Key Lab of Mobile Communications Technology, Chongqing University of Posts and Telecommunications, Chongqing, 400065, People’s Republic of China

    Tao Fan & Yun Lin

Authors
  1. Tao Fan
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Yun Lin
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Tao Fan.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Fan, T., Lin, Y. A Variable Step-Size Strategy Based on Error Function for Sparse System Identification. Circuits Syst Signal Process 36, 1301–1310 (2017). https://doi.org/10.1007/s00034-016-0344-1

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00034-016-0344-1

Keywords