A Low-Complexity Modulation Classification Algorithm for MIMO–OSTBC System

Abstract

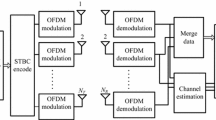
In this paper, a low-complexity modulation classification algorithm is proposed for the multiple-input multiple-output orthogonal space–time block code (MIMO–OSTBC) system. First, MIMO–OSTBC system is decoupled into several single-input single- output (SISO) systems by utilizing the orthogonal property of OSTBC. Then, these SISO systems are grouped into several two-input two- output systems. Finally, a maximum likelihood- based approach is used to classify the modulation. Both the cases of perfect and unknown channel state information (CSI) are considered. Simulations show that the proposed algorithm exhibits significantly lower complexity than conventional algorithm in both cases. Meanwhile, it provides better performance than conventional algorithm in the case of unknown CSI.

Appendix: The Proof for the Insensitivity of LF

Based on (15), we can obtain

$$\begin{aligned}&{\left[ {{\begin{array}{cc} {\mathbf{I}_n }&{} {j\mathbf{I}_n } \\ \end{array} }} \right] \,\mathbf{A}^{\mathrm{T}} \left( \hat{\mathbf{h}}\right) \mathbf{y}}/{\left\| {{\hat{\mathbf{h}}}} \right\| ^{2}} \nonumber \\&\quad ={\mathbf{DP}\left[ {{\begin{array}{cc} {\mathbf{I}_n }&{} {j\mathbf{I}_n } \\ \end{array} }} \right] \,\mathbf{A}^{\mathrm{T}}\mathbf{(h)y}}/{\left\| \mathbf{h} \right\| ^{2}} \nonumber \\&\quad ={\left[ {{\begin{array}{cc} {\mathbf{I}_n }&{} {j\mathbf{I}_n } \\ \end{array} }} \right] \left[ {{\begin{array}{c@{\quad }c} {\mathfrak {R}e\left( {\hat{\mathbf{D}}} {\hat{\mathbf{D}}}_q \right) \mathbf{P}}&{} {-\mathfrak {I}m\left( \hat{\mathbf{D}} {\hat{\mathbf{D}}}_q \right) \mathbf{P}} \\ {\mathfrak {I}m\left( {\hat{\mathbf{D}}} {\hat{\mathbf{D}}}_q \right) \mathbf{P}}&{} {\mathfrak {R}e\left( {\hat{\mathbf{D}}} {\hat{\mathbf{D}}_q } \right) \mathbf{P}} \\ \end{array} }} \right] \mathbf{A}^{\mathrm{T}}{} \mathbf{(h)y}}/{\left\| \mathbf{h} \right\| ^{2}} \end{aligned}$$

(20)

Then,

$$\begin{aligned} \mathbf{A(h)}={\mathbf{A}\left( \hat{\mathbf{h}}\right) }\left[ {{ \begin{array}{c@{\quad }c} {\left\{ {\mathfrak {R}e\left( {{\hat{\mathbf{D}}\hat{\mathbf{D}}}_q } \right) \mathbf{P}} \right\} ^{\mathrm{T}}}&{} {\left\{ {\mathfrak {I}m\left( {{\hat{\mathbf{D}}\hat{{\mathbf{D}}}}_q } \right) \mathbf{P}} \right\} ^{\mathrm{T}}} \\ {-\left\{ {\mathfrak {I}m\left( {{\hat{\mathbf{D}}\hat{{\mathbf{D}}}}_q } \right) \mathbf{P}} \right\} ^{\mathrm{T}}}&{} {\left\{ {\mathfrak {R}e\left( {{\hat{\mathbf{D}}\hat{{\mathbf{D}}}}_q } \right) \mathbf{P}} \right\} ^{\mathrm{T}}} \\ \end{array} }} \right] ^{-1} \end{aligned}$$

(21)

Therefore,

$$\begin{aligned} {\tilde{\tilde{\mathbf{y}}}}(v)= & {} \mathbf{A}^{\mathrm{T}}{\left( \hat{\mathbf{h}}\right) }{} \mathbf{y}(v)/{\left\| {\hat{\mathbf{h}}} \right\| }^{2}\nonumber \\= & {} \left[ {{\begin{array}{c@{\quad }c} {\mathfrak {R}e\left( {{\hat{\mathbf{D}}\hat{{\mathbf{D}}}}_q } \right) \mathbf{P}}&{} {-\mathfrak {I}m\left( {{\hat{\mathbf{D}}\hat{{\mathbf{D}}}}_q } \right) \mathbf{P}} \\ {\mathfrak {I}m\left( {{\hat{\mathbf{D}}\hat{{\mathbf{D}}}}_q } \right) \mathbf{P}}&{} {\mathfrak {R}e\left( {{\hat{\mathbf{D}}\hat{{\mathbf{D}}}}_q } \right) \mathbf{P}} \\ \end{array} }} \right] {\tilde{\mathbf{y}}}(v) \end{aligned}$$

(22)

where $\left\| {{\hat{\mathbf{h}}}} \right\| =\left\| \mathbf{h} \right\| =\sqrt{\hbox {tr}\left\{ {{\left[ {E\left( {\mathbf{YY}^{\mathrm{H}}-l\sigma ^{2}{} \mathbf{I}_{n_r } } \right) } \right] }/n} \right\} }$.

Next, we will prove that

$$\begin{aligned}&\sum _{v=1}^{N_b } {\sum _{u=1}^n {\log } \left\{ {\Lambda \left( {\left[ {\tilde{y}_u (v),\tilde{y}_{u+n} (v)} \right] |{\mathcal {M}}, \mathbf{H},\tilde{\sigma }^{2}} \right) } \right\} }\nonumber \\&\quad =\sum _{v=1}^{N_b } {\sum _{u=1}^n {\log } \left\{ {\Lambda \left( {\left[ {\tilde{\tilde{y}}_u (v),\tilde{\tilde{y}}_{u+n} (v)} \right] |{\mathcal {M}}, {\hat{\mathbf{H}}},{\hat{\mathbf{D}}},\tilde{\tilde{\sigma }}^{2}} \right) } \right\} } \end{aligned}$$

(23)

Proof

Due to $\begin{array}{l} \sum _{v=1}^{N_b } {\log \left\{ {\Lambda \left[ {{\tilde{\mathbf{y}}}(v)|\Theta , \mathbf{H}} \right] } \right\} } \\ =\sum _{v=1}^{N_b } {\log \left\{ {\Lambda \left[ {\left[ {{\begin{array}{c@{\quad }c} \mathbf{P}&{} \mathbf{P} \\ \mathbf{P}&{} \mathbf{P} \\ \end{array} }} \right] {\tilde{\mathbf{y}}}(v)|\Theta , \mathbf{H}} \right] } \right\} } \\ \end{array}$, the ambiguity resulted from $\mathbf{P}$ can be neglected.

Moreover,

$$\begin{aligned}&\sum _{u=1}^n {\log \left( {\sum _{s_u (v)\in {\mathcal {M}}} {\exp \left[ \frac{-\left| {\hbox {e}^{-j\hat{{\theta }}_u }\left( {\tilde{\tilde{y}}_u (v)+j\tilde{\tilde{y}}_{u+n} (v)} \right) -s_u (v)} \right| ^{2} }{\sigma ^{2}/ \left\| {\hat{\mathbf{h}}} \right\| ^{2}} \right] } } \right) } \nonumber \\&\quad =\sum _{u=1}^n \log \left( \sum _{s_u (v)\in {\mathcal {M}}} \exp \left[ \frac{-\left| {\hbox {e}^{j2\pi \rho _u /q}\left( {\tilde{y}_u (v)+j\tilde{y}_{u+n} (v)} \right) -s_u (v)} \right| ^2 }{{\sigma ^{2}}/{\left\| {{\hat{\mathbf{h}}}} \right\| ^{2}}} \right] \right) \nonumber \\&\quad =\sum _{u=1}^n {\log \left( {\sum _{s_u (v)\in {\mathcal {M}}} {\exp \left[ {\frac{-\left| {\left( {\tilde{y}_u (v)+j\tilde{y}_{u+n} (v)} \right) -\hbox {e}^{-j2\pi \rho _u /q}s_u (v)} \right| ^2 }{{\sigma ^{2}}/{\left\| \mathbf{h} \right\| ^{2}}}} \right] } } \right) } \nonumber \\&\quad =\sum _{u=1}^n {\log \left( {\sum _{s_u (v)\in {\mathcal {M}}} {\exp \left[ {\frac{-\left| {\left( {\tilde{y}_u (v)+j\tilde{y}_{u+n} (v)} \right) -s_u (v)} \right| ^2 }{{\sigma ^{2}}/{\left\| \mathbf{h} \right\| ^{2}}}} \right] } } \right) } \end{aligned}$$

(24)

Then, (23) is proved. $\square$