Skip to main content

Advertisement

Springer Nature Link
Log in

An Efficient \(L_{0}\) Norm Constraint Memory Improved Proportionate Affine Projection Algorithm

  • Short Paper
  • Published:
Circuits, Systems, and Signal Processing Aims and scope Submit manuscript

Abstract

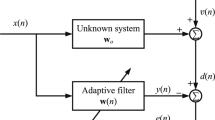
This paper proposes an \(L_{0}\) norm constraint memory improved proportionate affine projection algorithm with a lower computational complexity than the conventional \(L_{0}\) norm constraint improved proportionate affine projection algorithm. Particularly, to achieve a low computational complexity, we propose to remove the matrix before the zero attraction term. Moreover, the product of the proportionate matrix and input matrix is implemented using an efficient recursive scheme. Simulation results in acoustic echo cancellation context show that our algorithm not only significantly reduces the computational complexity but also achieves slightly improved steady-state misalignment.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  1. S.J.M. Almeida, J.C.M. Bermudez, N.J. Bershad, A stochastic model for a pseudo affine projection algorithm. IEEE Trans. Signal Process. 57(1), 107–118 (2009)

    Article  MathSciNet  Google Scholar 

  2. J. Benesty, S.L. Gay, An improved PNLMS algorithm, in IEEE ICASSP 2002, pp. 1881–1884

  3. M.Z.A. Bhotto, A. Antoniou, Affine-projection-like adaptive-filtering algorithms using gradient-based step size. IEEE Trans. Circuits Syst. I Regul. Pap. 61(7), 2048–2056 (2014)

    Article  Google Scholar 

  4. Y. Dong, H. Zhao, Y. Yu, Adaptive combination of proportionate NSAF with individual activation factors. Circuits Syst. Signal Process. doi:10.1007/s00034-016-0386-4

  5. Y. Gu, J. Jin, S. Mei, \(l_{0}\) norm constraint LMS algorithm for sparse system identification. IEEE Signal Process. Lett. 16(9), 774–777 (2009)

    Article  Google Scholar 

  6. S. Haykin, Adaptive Filter Theory (Prentice-Hall, Upper Saddle River, 2002)

    MATH  Google Scholar 

  7. O. Hoshuyama, R.A. Goubran, A. Sugiyama, A generalized proportionate variable step-size algorithm for fast changing acoustic environments, in IEEE ICASSP 2004, pp. 161–164

  8. M.V.S. Lima, T.N. Ferreira, W.A. Martins, P.S.R. Diniz, Sparsity-aware data-selective adaptive filters. IEEE Trans. Signal Process. 62(17), 4557–4572 (2014)

    Article  MathSciNet  Google Scholar 

  9. M.V.S. Lima, W.A. Martins, P.S.R. Diniz, Affine projection algorithms for sparse system identification, in IEEE ICASSP 2013, pp. 5666–5670

  10. Y. Liu, C. Li, Z. Zhang, Diffusion sparse least-mean squares over networks. IEEE Trans. Signal Process. 60(8), 4480–4485 (2012)

    Article  MathSciNet  Google Scholar 

  11. L. Lu, H. Zhao, A novel convex combination of LMS adaptive filter for system identification, in ICSP 2014, pp. 225–229

  12. L. Lu, H. Zhao, Z. He, B. Chen, A novel sign adaptation scheme for convex combination of two adaptive filters. Int. J. Electron. Commun. 69(11), 1590–1598 (2015)

    Article  Google Scholar 

  13. L. Lu, H. Zhao, C. Chen, A new normalized subband adaptive filter under minimum error entropy criterion. Signal Image Video Process. 10(6), 1097–1103 (2016)

    Article  Google Scholar 

  14. L. Lu, H. Zhao, Improved filtered-x least mean kurtosis algorithm for active noise control. Circuits Syst. Signal Process. (2016). doi:10.1007/s00034-016-0379-3

  15. K. Ozeki, T. Umeda, An adaptive filtering algorithm using an orthogonal projection to an affine subspace and its properties. Electron. Commun. Jpn. 67–A(5), 19–27 (1984)

    Article  MathSciNet  Google Scholar 

  16. C. Paleologu, S. Ciochina, J. Benesty, An efficient proportionate affine projection algorithm for echo cancellation. IEEE Signal Process. Lett. 17(2), 165–168 (2010)

    Article  Google Scholar 

  17. K. Pelekanakis, M. Chitre, New sparse adaptive algorithms based on the natural gradient and the \(L_{0}\)-norm. IEEE J. Ocean. Eng. 38(2), 323–332 (2013)

    Article  Google Scholar 

  18. A.H. Sayed, Fundamentals of Adaptive Filtering (Wiley, New York, 2003)

    Google Scholar 

  19. Y. Yu, H. Zhao, A band-independent variable step size proportionate normalized subband adaptive filter algorithm. Int. J. Electron. Commun. 70(9), 1179–1186 (2016)

    Article  Google Scholar 

  20. Y. Yu, H. Zhao, B. Chen, A new normalized subband adaptive filter algorithm with individual variable step sizes. Circuits Syst. Signal Process. 35(4), 1407–1418 (2016)

    Article  MathSciNet  Google Scholar 

  21. Y. Yu, H. Zhao, B. Chen, Sparse normalized subband adaptive filter algorithm with l0-norm constraint. J. Frankl. Inst. 353(18), 5121–5136 (2016)

    Article  MATH  Google Scholar 

  22. Y. Yu, H. Zhao, A joint-optimization NSAF algorithm based on the first-order Markov model. Signal Image Video Process. (2016). doi:10.1007/s11760-016-0988-0

  23. S. Zhang, J. Zhang, Transient analysis of zero attracting NLMS algorithm without Gaussian inputs assumption. Signal Process. 97, 100–109 (2014)

    Article  Google Scholar 

  24. S. Zhang, J. Zhang, H. Han, Robust variable step-size decorrelation normalized least-mean-square algorithm and its application to acoustic echo cancellation. IEEE/ACM Trans. Audio Speech Lang. Process. 24(12), 2368–2376 (2016)

    Article  Google Scholar 

  25. S. Zhao, Z. Man, S. Khoo, H.R. Wu, Stability and convergence analysis of transform-domain LMS adaptive filters with second-order autoregressive process. IEEE Trans. Signal Process. 57(1), 119–130 (2009)

    Article  MathSciNet  Google Scholar 

  26. H. Zhao, Z. Zheng, \(L_{0}\) norm constraint set-membership affine projection algorithm with coefficient vector reuse. Electron. Lett. 52(7), 560–562 (2016)

    Article  Google Scholar 

  27. H. Zhao, Z. Zheng, Bias-compensated affine-projection-like algorithms with noisy input. Electron. Lett. 52(9), 712–714 (2016)

    Article  Google Scholar 

  28. Z. Zheng, H. Zhao, Proportionate affine projection algorithm based on coefficient difference, in IEEE ICSPCC 2014, pp. 115–119

  29. Z. Zheng, H. Zhao, Memory improved proportionate M-estimate affine projection algorithm. Electron. Lett. 51(6), 525–526 (2015)

    Article  Google Scholar 

  30. Z. Zheng, H. Zhao, Affine projection M-estimate subband adaptive filters for robust adaptive filtering in impulsive noise. Signal Process. 120, 64–70 (2016)

    Article  Google Scholar 

  31. Z. Zheng, H. Zhao, Bias-compensated normalized subband adaptive filter algorithm. IEEE Signal Process. Lett. 23(6), 809–813 (2016)

    Article  Google Scholar 

Download references

Acknowledgements

The authors would like to thank the Editor and the reviewers for the valuable comments and suggestions. The authors would also like to thank Dr. Junbo Zhao (Virginia Polytechnic Institute and State University, USA) and other colleagues for polishing the language.

Author information

Authors and Affiliations

  1. School of Science, Lanzhou University of Technology, Lanzhou, China

    Zhaoxia Qu

  2. School of Electrical Engineering, Southwest Jiaotong University, Chengdu, China

    Zongsheng Zheng

Authors
  1. Zhaoxia Qu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Zongsheng Zheng
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Zhaoxia Qu.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Qu, Z., Zheng, Z. An Efficient \(L_{0}\) Norm Constraint Memory Improved Proportionate Affine Projection Algorithm. Circuits Syst Signal Process 36, 3448–3456 (2017). https://doi.org/10.1007/s00034-016-0467-4

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00034-016-0467-4

Keywords