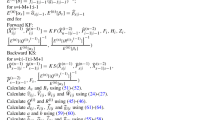Abstract
The sequential sample myriad has been proposed recently to estimate an unknown location parameter in real time by updating the current estimate when a new input sample is available. However, the algorithm is only capable of estimating an unknown constant (i.e., a time-invariant location parameter). In this paper, we propose a sequential myriad smoothing approach for tracking a time-varying location parameter corrupted by impulsive symmetric \(\alpha \)-stable noise. By incorporating exponential weighting factor to the sequential algorithm, the new algorithm weighs the recent samples more heavily to provide effective tracking capability. Simulation results show that the proposed method outperforms the classical exponential smoothing and is as good as the running myriad smoother.




Similar content being viewed by others
References
G.R. Arce, Nonlinear Signal Processing : A Statistical Approach (Wiley, New Jersey, 2005)
P.J. Brockwell, R.A. Davis, Introduction to Time Series and Forecasting (Springer, Berlin, 2002)
S.C. Chan, Y. Zou, A recursive least M-estimate algorithm for robust adaptive filtering in impulsive noise: fast algorithm and convergence analysis. IEEE Trans. Signal Process. 52(4), 975–991 (2004)
B. Chen, L. Xing, Z. Wu, J. Liang, J.C. Principe, N. Zheng, Smoothed least mean p-power error criterion for adaptive filtering. Digit. Signal Process. 40, 900–903 (2014)
B.M. Goh, H.S. Lim, Sequential algorithms for sample myriad and weighted myriad filter. IEEE Trans. Signal Process. 60(11), 6047–6052 (2012)
J.G. Gonzalez, Robust techniques for wireless communications in non-Gaussian environments. Dissertation, University of Delaware (1997)
J.G. Gonzalez, G.R. Arce, Optimality of the myriad filter in practical impulsive-noise environments. IEEE Trans. Signal Process. 49(2), 438–441 (2001)
J.G. Gonzalez, J.L. Paredes, G.R. Arce, Zero-order statistics: a mathematical framework for the processing and characterization of very impulsive signals. IEEE Trans. Signal Process. 54(10), 3839–3851 (2006)
J. He, Z. Liu, K.T. Wong, Linearly constrained minimum - “geometric power” adaptive beamforming using logarithmic moments of data containing heavy-tailed noise of unknown statistics. IEEE Antennas Wireless Propag. Lett 6, 600–603 (2007)
J. He, Z. Liu, K.T. Wong, Snapshot-instantaneous \(\vert \vert. \vert \vert \infty \) normalization against heavy-tail noise. IEEE Trans. Aerosp. Electron. Syst 44(3), 1221–1227 (2008)
S. Kalluri, G.R. Arce, Fast algorithms for weighted myriad computation by fixed-point search. IEEE Trans. Signal Process. 48(1), 159–171 (2000)
H.S. Lim, T.C. Chuah, H.T. Chuah, On the optimal alpha-k curve of the sample myriad. IEEE Signal Process. Lett. 14(8), 545–548 (2007)
R.G. Lyons, Understanding Digital Signal Processing (Prentice Hall, New Jersey, 2001)
R.C. Nunez, J.G. Gonzalez, G.R. Arce, J.P. Nolan, Fast and accurate computation of the myriad filter via branch-and-bound search. IEEE Trans. Signal Process. 56(7), 3340–3346 (2008)
T. Pander, Myriad filter computation with 2nd order approximation polynomial. Inf. Technol. Biomed. 69, 239–250 (2010)
A.A. Roenko, V.V. Lukin, I. Djurovic, Two approaches to adaptation of sample myriad to characteristics of \(\text{ S }\alpha \text{ S }\) distribution data. Signal Processing. 90(7), 2113–2123 (2010)
B. Yue, Z. Peng, Y.He, Q. Zhang, Impulsive noise suppression using fast myriad filter in seismic signal processing. in Proceedings of International Conference on Computational and Information Sciences (Shiyang, China, 2013)
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
1.1 Derivation of Exponential Myriad Smoothing
The myriad smoother \({\hat{\theta }}\left[ n \right] \) based on n observations is the solution of the following equation
Substituting \(\eta _i =\lambda ^{n-i}\), (11) can be written as
Let
The first-order Taylor series of \(\psi _\theta \left[ {n+1} \right] \) about the point \(\theta ={\hat{\theta }}\left[ n \right] \) is given by
where
Replacing \(\theta ={\hat{\theta }}\left[ {n+1} \right] \) in (14) and since \(\psi _{{\hat{\theta }}\left[ {n+1} \right] } \left[ {n+1} \right] \approx 0\), (14) can be rewritten as follows:
By using the definition of \(\psi _\theta \left[ n \right] \)in (13), we have
Substituting \(\theta \) with \({\hat{\theta }}\left[ n \right] \) and since \(\psi _{{\hat{\theta }}\left[ n \right] } \left[ n \right] \approx 0\), (17) can be rewritten as
Now, the problem is to find the updates that define \(\psi ^{{\prime }}_{{\hat{\theta }}\left[ n \right] } \left[ {n+1} \right] \) in terms of \(\psi ^{{\prime }}_{{\hat{\theta }}\left[ n-1 \right] } \left[ {n} \right] \). From (13) and (15), we have
Substituting \(\theta ={\hat{\theta }}\left[ n \right] \) in (19) yields
1.2 Convergence of Exponential Myriad Smoothing to Classical Exponential Smoothing
From (7), let \(\hbox {k}\rightarrow \infty \), and we have
Substituting (22) into (8), the following expression for \({\hat{J}} \left[ {n+1} \right] \) can be simplified as
Similarly, for the next iteration, \({\hat{J}} \left[ {n+2} \right] \) will be updated as
Hence, in general, for \(i\ge 1,\)
and
Consider \(i\rightarrow \infty \) and since \(\lambda <1\), then \(n\lambda ^{i}\rightarrow 0\) and \(\mathop \sum \nolimits _{m=0}^{i-1} \lambda ^{m}\rightarrow \frac{1}{1-\lambda }\)
1.3 Asymptotic Variance of the Exponential Myriad Smoothing
From (13), we have
where \(\psi _\theta \left( x \right) =\frac{\eta x}{k^{2}+x^{2}}\).
The asymptotic variance of exponential myriad smoother at a distribution F can be defined as
and \(\psi _\theta ^{\prime } \left( x \right) =\hbox {d}\psi _\theta \left( x \right) /\hbox {d}x\) [12].
Substituting \(\psi _\theta \left( x \right) =\frac{\eta x}{k^{2}+x^{2}}\) in (29) yields
where \(f_\alpha \left( x \right) \) is the distribution function. Eq. (31) shows that the exponential myriad smoother has the same asymptotic variance as the sample myriad given in [12].
Rights and permissions
About this article
Cite this article
Goh, B.M.K., Lim, H.S. & Tan, A.W.C. Exponential Myriad Smoothing Algorithm for Robust Signal Processing in \(\alpha \)-Stable Noise Environments. Circuits Syst Signal Process 36, 4468–4481 (2017). https://doi.org/10.1007/s00034-017-0523-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00034-017-0523-8