Abstract
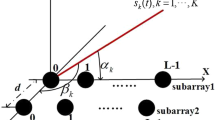
In this paper, an idea from the quasi-maximum-likelihood (QML) algorithm has been applied to estimation of the direction of arrival (DOA) and parameters of the polynomial phase signals (PPS) impinging on the uniform linear array. The algorithm uses a search over a set of possible DOA values. For considered value, the DOA is compensated and resulted signal parameters are estimated using the original QML approach. In this way, several sets of potential estimates are obtained. Optimal DOA and PPS parameters belong to set that maximizes the proposed cost function. In the proposed approach, parameters are estimated using 2-D search over DOA and window widths used for calculation of the short Fourier transform in the QML that is an important advantage with respect to existing strategies like, for example, the polynomial beamformer requiring multi-dimensional or metaheuristic search strategies. Numerical validation of the proposed approach for both mono- and multi-component signals is provided in the paper. Both far- and near-field scenarios are considered.





Similar content being viewed by others
References
A. Amar, Efficient estimation of a narrow-band polynomial phase signal impinging on a sensor array. IEEE Trans. Signal Process. 58(2), 923–927 (2010)
A. Amar, A. Leshem, A.J. van der Veen, A low complexity blind estimator of narrowband polynomial phase signals. IEEE Trans. Signal Process. 58(9), 4674–4683 (2010)
A. Belouchrani, M.G. Amin, Blind source separation based on time–frequency signal representations. IEEE Trans. Signal Process. 46(11), 2888–2897 (1998)
A. Belouchrani, M.G. Amin, N. Thirion-Moreau, Y.D. Zhang, Source separation and localization using time–frequency distributions: an overview. IEEE Signal Process. Mag. 30(6), 97–107 (2013)
B. Boashash, Time–Frequency Signal Analysis and Processing: A Comprehensive Reference (Academic Press, Salt Lake City, 2003)
B. Boashash, N.A. Khan, T. Ben-Jabeur, Time–frequency features for pattern recognition using high-resolution TFDs: a tutorial review. Digit. Signal Process. 40, 1–30 (2015)
S. Djukanović, M. Simeunović, I. Djurović, Efficient parameter estimation of polynomial-phase signals impinging on a sensor array, in 2012 Mediterranean Conference on Embedded Computing (MECO) (2012), pp. 116–119
S. Djukanović, M. Simeunović, I. Djurović, A low-complexity robust estimation of multiple wideband polynomial-phase signals in sensor array, in 2013 8th International Symposium on Image and Signal Processing and Analysis (ISPA) (IEEE, 2013), pp. 308–313
I. Djurović, On parameters of the QML PPS estimator. Signal Process. 116, 1–6 (2015)
I. Djurović, S. Djukanović, M. Simeunović, P. Raković, B. Barkat, An efficient joint estimation of wideband polynomial-phase signal parameters and direction-of-arrival in sensor array. EURASIP J. Adv. Signal Process. 2012(1), 1–10 (2012)
I. Djurović, M. Simeunović, Review of the quasi maximum likelihood estimator for polynomial phase signals. Digit. Signal Process. 72, 59–74 (2018)
I. Djurović, M. Simeunović, S. Djukanović, P. Wang, A hybrid CPF-HAF estimation of polynomial-phase signals: detailed statistical analysis. IEEE Trans. Signal Process. 60(10), 5010–5023 (2012)
I. Djurović, M. Simeunović, B. Lutovac, Are genetic algorithms useful for the parameter estimation of FM signals? Digit. Signal Process. 22(6), 1137–1144 (2012)
I. Djurović, LJ. Stanković, Quasi-maximum-likelihood estimator of polynomial phase signals. IET Signal Process. 8(4), 347–359 (2014)
I. Djurović, T. Thayaparan, LJ. Stanković, Adaptive local polynomial Fourier transform in ISAR. EURASIP J. Appl. Signal Process. 2006, 129–129 (2006)
I. Djurović, T. Thayaparan, LJ. Stanković, SAR imaging of moving targets using polynomial Fourier transform. IET Signal Process. 2(3), 237–246 (2008)
S. Elouaham, R. Latif, A. Dliou, M. Laaboubi, R.F.M. Maoulainie, Parametric and non parametric time–frequency analysis of biomedical signals. Int. J. Adv. Comput. Sci. Appl. 4(1), 74–79 (2013)
A.B. Gershman, M. Pesavento, M.G. Amin, Estimating parameters of multiple wideband polynomial-phase sources in sensor arrays. IEEE Trans. Signal Process. 49(12), 2924–2934 (2001)
A. Hassanien, A.B. Gershman, K.M. Wong, Estimating the parameters of multiple wideband polynomial-phase signals in sensor arrays using spatial time–frequency distributions, in IEEE International Conference on Acoustics, Speech and Signal Processing-ICASSP’07, vol. 2 (2007), pp. 1069–1072
Y.D. Huang, M. Barkat, Near-field multiple source localization by passive sensor array. IEEE Trans. Antennas Propag. 39(7), 968–975 (1991)
L. Inza, J. Mars, J.P. Métaxian, G.S. O’Brien, O. Macedo, Seismo-volcano source localization with triaxial broad-band seismic array. Geophys. J. Int. 187(1), 371–384 (2011)
C. Ioana, J.I. Mars, A. Serbanescu, S. Stanković, Time–frequency-phase tracking approach: application to underwater signals in a passive context, in 2010 IEEE International Conference on Acoustics, Speech and Signal Processing (IEEE, 2010), pp. 5634–5637
C. Ioana, A. Quinquis, Y. Stephan, Feature extraction from underwater signals using time–frequency warping operators. IEEE J. Ocean. Eng. 31(3), 628–645 (2006)
J.C. Lagarias, J.A. Reeds, M.H. Wright, P.E. Wright, Convergence properties of the Nelder–Mead simplex method in low dimensions. SIAM J. Optim. 9, 112–147 (1998)
C. Li, M. Liu, P. Wang, H. Wang, Subspace method to estimate parameters of wideband polynomial-phase signals in sensor arrays, in International Conference on Estimation, Detection and Information Fusion (ICEDIF) (2015), pp. 186–189
N. Linh-Trung, A. Belouchrani, K. Abed-Meraim, B. Boashash, Separating more sources than sensors using time–frequency distributions. EURASIP J. Appl. Signal Process. 2005, 2828–2847 (2005)
S. Liu, Y.D. Zhang, T. Shan, Detection of weak astronomical signals with frequency-hopping interference suppression. Digit. Signal Process. 72, 1–8 (2018)
S. Liu, Y.D. Zhang, T. Shan, R. Tao, Structure-aware Bayesian compressive sensing for frequency-hopping spectrum estimation with missing observations. IEEE Trans. Signal Process. 66(8), 2153–2166 (2018)
P. O’Shea, On refining polynomial phase signal parameter estimates. IEEE Trans. Aerosp. Electron. Syst. 46(3), 978–987 (2010)
S. Peleg, B. Porat, The Cramer–Rao lower bound for signals with constant amplitude and polynomial phase. IEEE Trans. Signal Process. 39(3), 749–752 (1991)
P. Raković, M. Simeunović, I. Djurović, On improvement of joint estimation of DOA and PPS coefficients impinging on ULA. Signal Process. 134, 209–213 (2017)
B. Ristić, B. Boashash, Comments on The Cramer–Rao lower bounds for signals with constant amplitude and polynomial phase. IEEE Trans. Signal Process. 46(6), 1708–1709 (1998)
LJ. Stanković, M. Daković, T. Thayaparan, Time–Frequency Signal Analysis with Applications (Artech House, Norwood, 2014)
LJ. Stanković, I. Djurović, S. Stanković, M. Simeunović, S. Djukanović, M. Daković, Instantaneous frequency in time–frequency analysis: enhanced concepts and performance of estimation algorithms. Digit. Signal Process. 35, 1–13 (2014)
O. Yilmaz, S. Rickard, Blind separation of speech mixtures via time–frequency masking. IEEE Trans. Signal Process. 52(7), 1830–1847 (2004)
X. Yuan, Direction-finding wideband linear FM sources with triangular arrays. IEEE Trans. Aerosp. Electron. Syst. 48(3), 2416–2425 (2012)
X. Yuan, Estimating the DOA and the polarization of a polynomial-phase signal using a single polarized vector-sensor. IEEE Trans. Signal Process. 60(3), 1270–1282 (2012)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 CRLB Derivation
The CRLB evaluation for signal model considered in the paper is addressed briefly. The CRLB derivations for case of a simplified array signal model are available in [18].
Our interest is to calculate the CRLB of parameter vector \(\mathbf {E} =[a_{0},a_{1},\dots ,a_{P}\), \(A,\tau ]\). Elements of vector \(\mathbf {E}\) are denoted by \(\mathbf {E}_{i}=a_{i}\), for \(i\in 0,\dots ,P\), \(E_{P+1}=A\), \(E_{P+2}=\tau \). The CRLB of \(\mathbf {E}_{i}\) is a diagonal element of the inverse Fisher information matrix \(\mathbf {F}\) on position \(\mathbf {F}_{i,i}\)
Elements of the Fisher information matrix are second-order partial derivatives of the log-likelihood function. For details related to the Fisher matrix determination, refer to [18, 30, 32]. In the following, we give summary of our derivations related to this matrix with \(F_{i,j}\) as the (i, j)th element of \((P+3)\times (P+3)\) matrix \(\mathbf {F}\):
Due to terms involving the ISD, we have evaluated the CRLB from (12) and (13) numerically.
1.2 NMS Method
Parameters of the proposed algorithm are refined in the final step using the NMS method. The NMS method finds minimum of the objective function using operations such as reflection, expansion, contraction and shrinking. Since our goal is function maximization, optimization function passed to the NMS method is \(\varGamma (\mathbf {g})=1/J(\upsilon ;b_{1},\dots ,b_{P}),\) where \(\mathbf {g}=[\upsilon ,b_{1},\dots ,b_{P}]\). The NMS method is summarized in Algorithm 4.
Standard values for the reflection, expansion, contraction and shrink coefficients are \(\alpha =1\), \(\gamma =2\), \(\rho =0.5\) and \(\varsigma =0.5\). Note that fminsearch function is MATLAB realization of the NMS method.

Rights and permissions
About this article
Cite this article
Djurović, I., Simeunović, M. & Raković, P. Quasi-maximum-Likelihood Estimator of PPS on the Uniform Linear Array. Circuits Syst Signal Process 38, 4874–4889 (2019). https://doi.org/10.1007/s00034-019-01095-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00034-019-01095-0