Skip to main content
SpringerLink
Log in

Convolution Theorem with Its Derivatives and Multiresolution Analysis for Fractional S-Transform

  • Published:
Circuits, Systems, and Signal Processing Aims and scope Submit manuscript

Abstract

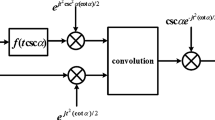
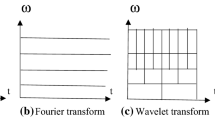
Fractional S-transform (FrST) is a time–frequency representation of signals with frequency-dependent resolution. FrST is also an advantageous technique for non-stationary signal processing applications. Till now, only linearity, scaling, time reversal, time marginal condition, and inverse FrST properties are documented. In this paper, some remaining properties of FrST are proposed to establish it as a complete transform technique. The proposed properties are convolution theorem, correlation theorem, and Parseval’s theorem. To expand the applicability of FrST as a mathematical transform tool, the multiresolution analysis concept is also documented. The multiresolution analysis has shown significant performance to develop the orthogonal kernel for FrST. Finally, the applications of proposed convolution theorem are demonstrated on multiplicative filtering for electrocardiogram signal and linear frequency-modulated signal under AWGN channel.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  1. O. Akay, G.F.B. Bartels, Fractional convolution and correlation via operator methods and an application to detection of linear FM signals. IEEE Trans. Signal Process. 49(5), 979–993 (2001)

    Article  Google Scholar 

  2. R.A. Brown, R. Fayne, in A fast discrete S-transform for biomedical signal processing. International IEEE EMBS Conference (IEEE, 2008), pp. 2586-2589

  3. D.R. Chen, D.H. Xiang, A construction of multiresolution analysis on interval. Acta Mathematica Sinica 23(4), 705–710 (2007)

    Article  MathSciNet  Google Scholar 

  4. D.Z. Cong, X.D. Ping, Z.J. Ming, Application to reservoir prediction and fluid identification. Appl. Geophys. 13(2), 343–352 (2016)

    Article  Google Scholar 

  5. X. Dai, Y. Diao, Q. Gu, D. Han, Wavelets with frame multiresolution analysis. J. Fourier Anal. Appl. 9, 39–48 (2003)

    Article  MathSciNet  Google Scholar 

  6. E. Furman, On the convolution of the negative binomial random variables. Stat. Probab. Lett. 77, 169–172 (2007). https://doi.org/10.1016/j.spl.2006.06.007

    Article  MathSciNet  MATH  Google Scholar 

  7. B.G. Goodyear, H. Zhu, R.A. Brown, J.R. Mitchell, Removal of phase artefacts from fMRI data using a Stockwell transform filter improves brain activity detection. Magn. Reson. Med. 51(1), 16–21 (2004)

    Article  Google Scholar 

  8. S. Granieri, R. Arizaga, E.E. Sicre, Optical correlation based on the fractional Fourier transform. Appl. Opt. 36(26), 6636–6645 (1997)

    Article  Google Scholar 

  9. S.S. Kelkar, L.L. Grigsby, J. Langsner, An extension of Parseval’s theorem and its use in calculating transient energy in the frequency domain. IEEE Trans. Ind. Electr. 30(1), 42–45 (1983)

    Article  Google Scholar 

  10. H. Khosravani, C.R. Pinnegar, J.R. Mitchell, B.L. Bardakjian, P. Federico et al., Increased high frequency oscillations precede in vitro low Mg + 2Seizures. Epilepsia 46(8), 1361–1372 (2005)

    Article  Google Scholar 

  11. S. Liu, T. Shan, R. Tao, Y.D. Zhang, G. Zhang, F. Zhang, Y. Wang et al., Sparse discrete fractional Fourier transform and its applications. IEEE Trans. Signal Process. 62(24), 6582–6595 (2014)

    Article  MathSciNet  Google Scholar 

  12. W. Lu, F. Li, Seismic spectral decomposition using deconvolutive short-time Fourier transform spectrogram. Geophysics 78(2), V43–V51 (2013)

    Article  Google Scholar 

  13. S.F. Lukomskii, Riesz multiresolution analysis on vilenkin groups. Doklady Math. 90, 412–415 (2014)

    Article  MathSciNet  Google Scholar 

  14. D.M. Mech, A. Cariow, A low-complexity approach to computation of the discrete fractional Fourier transform. Circuits Syst. Signal Process. 36, 4118–4144 (2017)

    Article  Google Scholar 

  15. D. Mendlovic, H.M. Ozaktas, A.W. Lohmann, Fractional correlation. Appl. Opt. 34(2), 303–309 (1995)

    Article  Google Scholar 

  16. H.M. Ozaktas, B. Barshan, Convolution, filtering, and multiplexing in fractional Fourier domains and their relation to chirp and wavelet transforms. J. Opt. Soc. Am. 11(2), 547–559 (1994)

    Article  MathSciNet  Google Scholar 

  17. S.C. Pei, J.J. Ding, Closed-form discrete fractional Fourier transform. IEEE Trans. Signal Process. 48(5), 1338–1353 (2000)

    Article  MathSciNet  Google Scholar 

  18. X.D. Ping, G. Ke, Fractional S-transform. Appl. Geophys. 9(1), 73–79 (2012)

    Article  MathSciNet  Google Scholar 

  19. C.R. Pinneger, J.R. Mitchell, Method and system for signal processing using sparse approximation of the S-transform. US Patent Application. #11/442, 991 (2006)

  20. R. Rangayan, Biomedical Signal Analysis A Case-Study Approach (Wiley, Hoboken, 2009)

    Google Scholar 

  21. C.D. Sarris, L.P.B. Katehi, J.F. Harvey, Application of multiresolution analysis to the modeling of microwave and optical structures. Opt. Quant. Electron. 32, 657–679 (2000)

    Article  Google Scholar 

  22. J. Shi, X. Liu, N. Zhang, Multiresolution analysis and orthogonal wavelets associated with fractional wavelet transform. Signal Image Video Process. 9(1), 211–220 (2015)

    Article  Google Scholar 

  23. J. Shi, Y. Chi, N. Zhang, Multichannel sampling and reconstruction of bandlimited signals in fractional Fourier domain. IEEE Signal Process. Lett. 17, 909–912 (2012)

    Google Scholar 

  24. A. Singh, Fractional S-transform for Boehmians. J. Anal. Number Theory. 3(2), 103–108 (2015)

    Article  Google Scholar 

  25. S.K. Singh, The fractional S-transform on space of type S. J. Math. 2013, 1–9 (2013)

    Article  MathSciNet  Google Scholar 

  26. S.K. Singh, The fractional S-transform on space of type W. J. Pseudo Differ. Oper. Appl. 4, 251–265 (2013)

    Article  MathSciNet  Google Scholar 

  27. R. Wang, Edge detection using convolutional neural network L. Cheng et al. (Eds.): ISNN 2016. LNCS 97(19), 12–20 (2016)

    Google Scholar 

  28. D. Wel, Q. Ran, Multiplicative filtering in the fractional Fourier domain. Signal Image and Video Process. 7, 575–580 (2013)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Electronics and Communication Engineering, Thapar Institute of Engineering and Technology, Patiala, Punjab, India

    Rajeev Ranjan, A. K. Singh & Neeru Jindal

Authors
  1. Rajeev Ranjan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. K. Singh
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Neeru Jindal
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Rajeev Ranjan.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ranjan, R., Singh, A.K. & Jindal, N. Convolution Theorem with Its Derivatives and Multiresolution Analysis for Fractional S-Transform. Circuits Syst Signal Process 38, 5212–5235 (2019). https://doi.org/10.1007/s00034-019-01118-w

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00034-019-01118-w

Keywords

Search

Navigation