Abstract
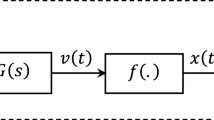
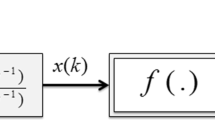
The Wiener nonlinear system is composed of a linear dynamic subsystem in series with a static nonlinear subsystem. This type of system is widely found in the petroleum, chemistry, thermal and other process industries. It is of great significance to obtain the parameter estimates of the Wiener systems. This paper studies the identification problem of the Wiener time delay nonlinear system. Based on the gradient search principle, a stochastic gradient identification algorithm and a gradient-based iterative identification algorithm are derived. Furthermore, a linearly decreasing weight particle swarm iterative identification algorithm is also proposed for the discussed Wiener time delay systems. Finally, a numerical example and two application cases are given for validating the feasibility of the three identification methods. The results demonstrate that the three algorithms can identify the unknown parameters of the Wiener model effectively. Moreover, the linearly decreasing weight particle swarm iterative identification algorithm behaves much better than the stochastic gradient and the gradient-based iterative algorithms in accuracy and convergence speed.











Similar content being viewed by others
References
A. Alfi, M.M. Fateh, Intelligent identification and control using improved fuzzy particle swarm optimization. Expert Syst. Appl. 38(10), 12312–12317 (2011)
Z. Alkhoury, M. Petreczky, G. Mercère, Identifiability of affine linear parameter-varying models. Automatica 80, 62–74 (2017)
S. Alonso, M. De la Sen, R. Nistal, A. Ibeas, Discretization and control of an SEIR epidemic model under equilibrium Wiener noise disturbances. AIP Conf. Proc. 1905(1), 030007 (2017)
H. Ase, T. Katayama, A subspace-based identification of Wiener–Hammerstein benchmark model. Control Eng. Pract. 44, 126–137 (2015)
M. Benítez, A. Bermúdez, J.F. Rodríguez-Calo, Adjoint method for parameter identification problems in models of stirred tank chemical reactors. Chem. Eng. Res. Des. 123, 214–229 (2017)
M.R. Bonyadi, Z. Michalewicz, Particle swarm optimization for single objective continuous space problems: a review. Evol. Comput. 25(1), 1–54 (2017)
G. Bottegal, R. Castro-Garcia, J.A.K. Suykens, A two-experiment approach to Wiener system identification. Automatica 93, 282–289 (2018)
G.A. Bustos, A. Ferramosca, J.L. Godoy, A.H. González, Application of model predictive control suitable for closed-loop re-identification to a polymerization reactor. J. Process Control 44, 1–13 (2016)
N.I. Chaudhary, M.A.Z. Raja, Identification of Hammerstein nonlinear ARMAX systems using nonlinear adaptive algorithms. Nonlinear Dyn. 79(2), 1385–1397 (2015)
J. Chen, J. Li, Y.J. Liu, Gradient iterative algorithm for dual-rate nonlinear systems based on a novel particle filter. J. Frankl. Inst. 354(11), 4425–4437 (2017)
M. De la Sen, S. Alonso-Quesada, A. Ibeas, On the stability of an SEIR epidemic model with distributed time-delay and a general class of feedback vaccination rules. Appl. Math. Comput. 270, 953–976 (2015)
F. Ding, X.M. Liu, M.M. Liu, The recursive least squares identification algorithm for a class of Wiener nonlinear systems. J. Frankl. Inst. 353(7), 1518–1526 (2016)
F. Ding, X.H. Wang, Q.J. Chen, Y.S. Xiao, Recursive least squares parameter estimation for a class of output nonlinear systems based on the model decomposition. Circuits Syst. Signal Process. 35(9), 3323–3338 (2016)
F. Ghani, R. Waser, T.S. O’Donovan, P. Schuetz, M. Zaglio, J. Wortischek, Non-linear system identification of a latent heat thermal energy storage system. Appl. Therm. Eng. 134, 585–593 (2018)
Y. Ghoul, K.I. Taarit, M. Ksouri, Identification of continuous-time systems with multiple unknown time delays using an output error method from sampled data. Circuits Syst. Signal Process. 37(3), 1044–1061 (2018)
G.C. Goodwin, K.S. Sin, Adaptive Filtering Prediction and Control (Prentice-Hall Information, Upper Saddle River, 1984)
A. Gotmare, R. Patidar, N.V. George, Nonlinear system identification using a cuckoo search optimized adaptive Hammerstein model. Expert Syst. Appl. 42(5), 2538–2546 (2015)
H. Kargar, J. Zarei, R. Razavi-Far, Robust fault detection filter design for nonlinear networked control systems with time-varying delays and packet dropout. Circuits Syst. Signal Process. 38(1), 63–84 (2019)
V.A. Kazakov, A method of measuring current–voltage characteristics based on the Hammerstein–Chebyshev model. Meas. Tech. 47(5), 494–499 (2004)
M. Kazemi, M.M. Arefi, A fast iterative recursive least squares algorithm for Wiener model identification of highly nonlinear systems. ISA Trans. 67, 382–388 (2017)
J. Kennedy, R. Eberhart, Particle swarm optimization, in Proceedings of the Fourth IEEE International Conference on Neural Networks (Australia, IV, Perth, 1995), pp. 1942–1948
J.H. Li, X. Li, Particle swarm optimization iterative identification algorithm and gradient iterative identification algorithm for Wiener systems with colored noise. Complexity 2018, 1–8 (2018)
J.S. Lu, W.D. Xie, H.B. Zhou, Combined fitness function based particle swarm optimization algorithm for system identification. Comput. Ind. Eng. 95, 122–134 (2016)
H. Modares, A. Alfi, M.N. Sistani, Parameter estimation of bilinear systems based on an adaptive particle swarm optimization. Eng. Appl. Artif. Intel. 23(7), 1105–1111 (2010)
M.J. Moghaddam, H. Mojallali, M. Teshnehlab, Recursive identification of multiple-input single-output fractional-order Hammerstein model with time delay. Appl. Soft Comput. 70, 486–500 (2018)
G. Mzyk, P. Wachel, Kernel-based identification of Wiener–Hammerstein system. Automatica 83, 275–281 (2017)
A. Naitali, F. Giri, Wiener-Hammerstein system identification-an evolutionary approach. Int. J. Syst. Sci. 47(1), 45–61 (2016)
K.S. Narendra, A.M. Annaswamy, Persistent excitation in adaptive systems. Int. J. Control 45(1), 127–160 (1987)
A. Nickabadi, M.M. Ebadzadeh, R. Safabakhsh, A novel particle swarm optimization algorithm with adaptive inertia weight. Appl. Soft Comput. 11(4), 3658–3670 (2011)
P.S. Pal, R. Kar, D. Mandal, S.P. Ghoshal, Parametric identification with performance assessment of Wiener systems using brain storm optimization algorithm. Circuits Syst. Signal Process. 36(8), 3143–3181 (2017)
K. Tiels, J. Schoukens, Wiener system identification with generalized orthonormal basis functions. Automatica 50(12), 3147–3154 (2014)
A. Wills, T.B. Schön, L. Ljung, B. Ninness, Identification of Hammerstein–Wiener models. Automatica 49(1), 70–81 (2013)
W.L. Xiong, X.Q. Yang, L. Ke, B.G. Xu, EM algorithm-based identification of a class of nonlinear Wiener systems with missing output data. Nonlinear Dyn. 80(1–2), 329–339 (2015)
G. Xu, G.S. Yu, Reprint of: on convergence analysis of particle swarm optimization algorithm. J. Comput. Appl. Math. 340, 709–717 (2018)
Y.Z. Yu, X.Y. Ren, F.S. Du, J.J. Shi, Application of improved PSO algorithm in hydraulic pressing system identification. J. Iron Steel Res. Int. 19(9), 29–35 (2012)
J.H. Zhang, P.Q. Xia, An improved PSO algorithm for parameter identification of nonlinear dynamic hysteretic models. J. Sound Vib. 389, 153–167 (2017)
Y.X. Zheng, Y. Liao, Parameter identification of nonlinear dynamic systems using an improved particle swarm optimization. Optik 127(19), 7865–7874 (2016)
Acknowledgements
This work was supported in part by the National Natural Science Foundation of China (61973176, 61973178), the Jiangsu Natural Science Foundation (BK20181457), the Natural science foundation for colleges and universities in Jiangsu Province (18KJB120007) and the Six Talent Peak Projects in Jiangsu Province (XYDXX-038).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Li, J., Zong, T., Gu, J. et al. Parameter Estimation of Wiener Systems Based on the Particle Swarm Iteration and Gradient Search Principle. Circuits Syst Signal Process 39, 3470–3495 (2020). https://doi.org/10.1007/s00034-019-01329-1
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00034-019-01329-1