Efficient Clustering of Non-coherent and Coherent Components Regardless of Sources’ Powers for 2D DOA Estimation

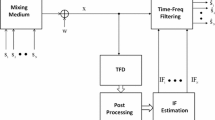
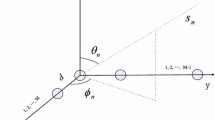
Abstract

Conventional decorrelation techniques that resolve all signals simultaneously are not efficient in mixture scenarios of non-coherent and coherent signals. In newer methods for one-dimensional arrays, non-coherent signals and coherent groups are resolved separately. However, employing an unreliable and non-adaptive threshold is the most significant disadvantage of these methods. On the other hand, they cannot be implemented for two-dimensional arrays. To deal with these issues, the signals separation using k-medoids clustering (SSKMC) algorithm was presented. Although the SSKMC algorithm does not have any of the shortcomings mentioned above, it relies on a basic limiting assumption that the sources should be equi-power. Therefore, the practical application of the SSKMC algorithm is facing a serious problem. In this paper, the SSKMC algorithm is extended so that it can be used even if the sources’ powers are not the same. First, the two-dimensional array is divided into several parallel linear sub-arrays. Then, by defining a components separation matrix, and employing its eigenvalues, the non-coherent and coherent components are identified. The effectiveness of the proposed solution is proven by mathematical facts. Simulation results verify the proofs and the benefit of the proposed solution.

Appendix: Proof of Inequality \( \left| {\iota_{{K_{n} + g}} } \right| < 1 \)

Given Eq. (24), the triangular inequality and the fact that $\left| {e^{{j\frac{2\pi }{\lambda }d_{y} \cos \theta_{{\left( {K_{n} + g} \right)i}} \sin \varphi_{{\left( {K_{n} + g} \right)i}} }} } \right| = 1$, we have

$$ \left| {\iota_{{K_{n} + g}} } \right| = \left| {\beta_{g1} e^{{j\frac{2\pi }{\lambda }d_{y} \cos \theta_{{\left( {K_{n} + g} \right)1}} \sin \varphi_{{\left( {K_{n} + g} \right)1}} }} \alpha_{g1} + \cdots} \right.\left. { + \beta_{{gp_{g} }} e^{{j\frac{2\pi }{\lambda }d_{y} \cos \theta_{{\left( {K_{n} + g} \right)p_{g} }} \sin \varphi_{{\left( {K_{n} + g} \right)p_{g} }} }} \alpha_{{gp_{g} }} } \right| < \left| {\beta_{g1} \alpha_{g1} } \right| + \cdots + \left| {\beta_{{gp_{g} }} \alpha_{{gp_{g} }} } \right|. $$

(26)

Note that since, according to [A4], for $i,\,i^{\prime} = 1,\,\ldots,\,p_{g}$ and $i \ne i^{\prime}$, we have $\cos \theta_{{\left( {K_{n} + g} \right)i}} \sin \varphi_{{\left( {K_{n} + g} \right)i}} \ne \cos \theta_{{\left( {K_{n} + g} \right)i^{\prime} }} \sin \varphi_{{\left( {K_{n} + g} \right)i^{\prime} }}$, so the equality does not hold in triangular inequality. On the other hand, since ${\varvec{\upbeta}}_{g} = {\varvec{\upalpha}}_{g}^{\dag }$, $\beta_{gp}$ s can be calculated in terms of the FCs as follows:

$$ \left[ {\beta_{g1} ,\,\ldots,\,\beta_{{gp_{g} }} } \right] = \left( {\left[ {\alpha_{g1}^{*} ,\,\ldots,\,\alpha_{{gp_{g} }}^{*} } \right]\left[ {\alpha_{g1} ,\,\ldots,\,\alpha_{{gp_{g} }} } \right]^{T} } \right)^{ - 1} \left[ {\alpha_{g1}^{*} ,\,\ldots,\,\alpha_{{gp_{g} }}^{*} } \right] = \frac{{\left[ {\alpha_{g1}^{*} ,\,\ldots,\,\alpha_{{gp_{g} }}^{*} } \right]}}{{\left| {\alpha_{g1} } \right|^{2} + \cdots + \left| {\alpha_{{gp_{g} }} } \right|^{2} }}. $$

(27)

So, $\beta_{gp}$ can be written as

$$ \beta_{gp} = \frac{{\alpha_{gp}^{*} }}{{\left| {\alpha_{g1} } \right|^{2} + \cdots + \left| {\alpha_{{gp_{g} }} } \right|^{2} }}. $$

(28)

Consequently, according to Eqs. (25) and (27), we can write

$$ \left| {\iota_{{K_{n} + g}} } \right| < \frac{{\left| {\alpha_{g1} } \right|^{2} }}{{\left| {\alpha_{g1} } \right|^{2} + \cdots + \left| {\alpha_{{gp_{g} }} } \right|^{2} }} + \cdots + \frac{{\left| {\alpha_{{gp_{g} }} } \right|^{2} }}{{\left| {\alpha_{g1} } \right|^{2} + \cdots + \left| {\alpha_{{gp_{g} }} } \right|^{2} }} = 1. $$

(29)

So, the inequality is proved.