Skip to main content
Springer Nature Link
Log in

Chaotic or Hyper-chaotic Oscillator? Numerical Solution, Circuit Design, MATLAB HDL-Coder Implementation, VHDL Code, Security Analysis, and FPGA Realization

  • Published:
Circuits, Systems, and Signal Processing Aims and scope Submit manuscript

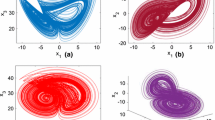
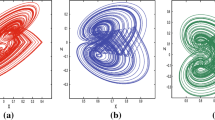
Abstract

Hyper-chaotic systems can exhibit a higher level of complexity in comparison with the chaotic systems. However, they require more resources when they are realized on a modular field-programmable gate array (FPGA). In this paper, we introduce full hardware/software comparison and security analysis of three-dimensional chaotic and four-dimensional hyper-chaotic oscillator systems. The two systems (previously implemented only in analog form) are realized on a modular FPGA hardware platform to generate high-speed random bit-streams. The realization is performed using two versions of VHDL code, one is generated automatically using a MATLAB HDL-Coder, and the optimized one which is manually written. The work explores the features of each oscillator system such as throughput, FPGA resources utilization, operating clock frequency, and security of the generated bit-streams, to show a compromise solution on these features. The experimental results show that the hyper-chaotic oscillator has higher level of security than the chaotic one, but it is slower and utilizes more FPGA resources. However, when the overall comparison measure figure of merit (FOM) is used, the chaotic system shows 188% better FOM than the hyper-chaotic system (for the automatically generated version) and 183% (for the manually written one).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

Data Availability

This study has no associated data.

References

  1. F. Almutairi, T. Bonny, new image encryption algorithm based on switching-type chaotic oscillator, in IEEE International Conference on Electrical and Computing Technologies and Applications, Ras Al Khaimah, UAE, November 2019 (2019)

  2. L. Avalos-Ruiz, C. Zuniga-Aguilar et al., FPGA implementation and control of chaotic systems involving the variable-order fractional operator with Mittag–Leffler law. Chaos Solitons Fract. 115, 177–189 (2018)

    MathSciNet  MATH  Google Scholar 

  3. J.M. Bahi, X. Fang, C. Guyeux, L. Larger, FPGA design for pseudorandom number generator based on chaotic iteration used in information hiding application. Appl. Math. Inf. Sci. 7(6), 2175–2188 (2013)

    MathSciNet  Google Scholar 

  4. T. Bonny, et al., An adaptive hybrid multiprocessor technique for bioinformatics sequence alignment, in International Conference on Biomedical Engineering Conference (2010)

  5. T. Bonny, J. Henkel, LICT: left-uncompressed instructions compression technique to improve the decoding performance of VLIW processors, in Design Automation Conference (DAC09), USA, pp. 903–906 (2009)

  6. T. Bonny, A.S. Elwakil, FPGA realizations of high speed switching-type chaotic oscillators using compact VHDL codes. J. Nonlinear Dyn. 93, 819–833 (2018)

    Google Scholar 

  7. T. Bonny, J. Henkel, Instruction re-encoding facilitating dense embedded code. Des. Autom. Test Eur. 4484772, 770–775 (2008)

    Google Scholar 

  8. T. Bonny, Q. Nasir, Clock glitch fault injection attack on an FPGA-based non-autonomous chaotic oscillator. Nonlinear Dyn. 96(3), 2087–2101 (2019)

    Google Scholar 

  9. T. Bonny, T. Rabie, A.H.A. Hafez, Multiple histogram-based face recognition with high speed FPGA implementation. Multimed. Tools Appl. 77(18), 24269–24288 (2018)

    Google Scholar 

  10. T. Bonny, R. Aldebsi, S. Majzoub, A. Elwakil, Hardware optimized FPGA implementations of high speed true random bit generators based on switching-type chaotic oscillators. J. Circuits Syst. Signal Process. 38, 1342–1359 (2019)

    Google Scholar 

  11. G. Chen, T. Ueta, Yet another chaotic attractor. Int. J. Bifurc. Chaos 9, 1465–1466 (1999)

    MathSciNet  MATH  Google Scholar 

  12. S.-L. Chen, T. Hwang, S.-M. Chang, W.-W. Lin, A fast digital chaotic generator for secure communication. Int. J. Bifurc. Chaos 20, 119 (2010)

    MathSciNet  MATH  Google Scholar 

  13. A. Coronel-Escamilla, J.F. Gomez-Aguilar, L. Torres, R.F. Escobar-Jimenez, M. Valtierra-Rodriguez, Synchronization of chaotic systems involving fractional operators of Liouville–Caputo type with variable-order. Physica A 487, 1–21 (2017)

    MathSciNet  Google Scholar 

  14. L. De Micco, H.A. Larrondo, Methodology for FPGA implementation of a chaos-based AWGN generator, in Field-Programmable Gate Array (FPGA) Technologies for High Performance Instrumentation, ed. by J.D.D. Gazzano (IGI Global, Hershey, 2016)

    Google Scholar 

  15. L. Dieci, Jacobian free computation of Lyapunov exponents. J. Dyn. Differ. Equ. 14(3), 697–717 (2002)

    MathSciNet  MATH  Google Scholar 

  16. Digilent, Inc, www.zedboard.org (2016). Accessed 2020

  17. S. Ergun, S. Ozoguz, Truly random number generators based on a non-autonomous chaotic oscillator. Int. J. Electron. Commun. 61, 235–242 (2007)

    Google Scholar 

  18. J.E. Escalante-Martínez, J.F. Gomez-Aguilar, C. Calderon-Ramon, A. Aguilar-Melendez, P. Padilla-Longoria, A mathematical model of circadian rhythms synchronization using fractional differential equations system of coupled van der Pol oscillators. Int. J. Biomath. 11(01), Article 1850014 (2018)

    MathSciNet  MATH  Google Scholar 

  19. X. Fang, Q. Wang, C. Guyeux, J.M. Bahi, FPGA acceleration of a pseudorandom number generator based on chaotic iterations. J. Inf. Secur. Appl. 19(1), 78–87 (2014)

    Google Scholar 

  20. R.L. Filali, M. Benrejeb, P. Borne, Observer-based secure communication design using discrete-time hyperchaotic systems. Commun. Nonlinear Sci. Numer. Simul. 19(5), 1424–1432 (2014)

    MathSciNet  MATH  Google Scholar 

  21. A.L. Fitch, D. Yu, H.H.C. Iu, V. Sreeram, Hyperchaos in an memristor-based modified canonical Chua’s circuit. Int. J. Bifurc. Chaos 22, 1250133–8 (2012)

    MATH  Google Scholar 

  22. R. Gupta, A. Pandey, R.K. Baghel, FPGA implementation of chaos-based high-speed true random number generator. Int. J. Numer. Modell. Electron. Netw. Devices Fields 2019, e2604 (2019)

    Google Scholar 

  23. http://csrc.nist.gov/groups/ST/toolkit/rng/documentation_software.html. Accessed 2020

  24. https://www.nutaq.com/matlab-hdl-coder-xilinx-system-generator. Accessed 2020

  25. Inc, X.: 7 Series FPGAs Overview, vol. 1. Xilinx (2014)

  26. M.P. Kennedy, Robust OP AMP realization of Chua’s circuit. Frequenz 46, 66–80 (1992)

    Google Scholar 

  27. M.P. Kennedy, Chaos in the Colpitts oscillator. IEEE Trans. Circuits Syst. I Fund. Theor. Appl. 41, 771–774 (1994)

    Google Scholar 

  28. J.M. Kowalski, G.L. Albert, G.W. Gross, Asymptotically synchronous chaotic orbits in systems of excitable elements. Phys. Rev. A 42(10), 6260–6263 (1990)

    Google Scholar 

  29. I. Koyuncu, A.T. Ozcerit, The design and realization of a new high speed FPGA-based chaotic true random number generator. Comput. Electr. Eng. 58, 203–214 (2017)

    Google Scholar 

  30. I. Koyuncu, A.T. Ozcerit, I. Pehlivan, Implementation of FPGA-based real time novel chaotic oscillator. Nonlinear Dyn. 77(1–2), 49–59 (2014)

    MathSciNet  Google Scholar 

  31. I. Koyuncu, M. Tuna, I. Pehlivan, C.B. Fidan, M. Alçın, Design, FPGA implementation and statistical analysis of chaos-ring based dual entropy core true random number generator. Analog Integr. Circuits Signal Process. 102, 445–456 (2020)

    Google Scholar 

  32. C.-Y. Li, Y.-H. Chen, T.-Y. Chang, L.-Y. Deng, K. To, Period extension and randomness enhancement using high-throughput reseeding-mixing PRNG. IEEE Trans. Very Large Scale Integr. Syst. 20, 38538 (2012)

    Google Scholar 

  33. Q. Li, H. Shiyi, S. Tang, G. Zeng, Hyperchaos and horseshoe in a 4D memristive system with a line of equilibria and its implementation. Int. J. Circ. Theor. Appl. 42, 1172–1188 (2014)

    Google Scholar 

  34. J. Ma, P. Zhou, B. Ahmad, G. Ren, C. Wang, Chaos and multi-scroll attractors in RCL-shunted junction coupled Jerk circuit connected by memristor. PLoS ONE 13(1), e0191120 (2018)

    Google Scholar 

  35. M. Park, J.C. Rodgers, D.P. Lathrop, True random number generation using CMOS Boolean chaotic. Microelectron. J. 46(12), 1364–1370 (2015)

    Google Scholar 

  36. V.T. Pham, S. Vaidyanathan, C. Volos, E. Tlelo-Cuautle, F.R. Tahir, A memristive system with hidden attractors and its engineering application, in Advances in Memristors, Memristive Devices and Systems, vol. 701, Studies in Computational Intelligence, ed. by S. Vaidyanathan, C. Volos (Springer, Cham, 2017)

    Google Scholar 

  37. M. Qiu, S. Yu, Y. Wen et al., Design and FPGA implementation of a universal chaotic signal generator based on the Verilog HDL fixed-point algorithm and state machine control. Int. J. Bifurc. Chaos 27(3), 1750040–1750055 (2017)

    MATH  Google Scholar 

  38. A.A. Rezk, A.H. Madian, A.G. Radwan, A.M. Soliman, Reconfigurable chaotic pseudo random number generator based on FPGA. AEU Int. J. Electron. Commun. 98, 174–180 (2018)

    Google Scholar 

  39. O.E. Rossler, An equation for continuous chaos. Phys. Lett. A 57, 397–398 (1976)

    MATH  Google Scholar 

  40. O.E. Rossler, An equation for hyperchaos. Phys. Lett. A 71, 155–157 (1979)

    MathSciNet  MATH  Google Scholar 

  41. A. Rukhin, et al., A statistical test suite for random and pseudorandom number generators for cryptographic applications, NIST Special Publication 800-22 (2001)

  42. B. Sunar, True random number generators for cryptography, Cryptographic Engineering (Springer, Boston, 2009). https://doi.org/10.1007/978-0-387-71817-0_4

    Chapter  Google Scholar 

  43. E. Tlelo-Cuautle, A. Quintas-Valles, L. de la Fraga, J. Rangel-Magdaleno, VHDL descriptions for the FPGA implementation of PWL-function-based multi-scroll chaotic oscillators. PLoS ONE 11(12), e0168300 (2016)

    Google Scholar 

  44. M.F. Tolba, A.S. Elwakil, H. Orabi, M. Elnawawy, F. Aloul, A. Sagahyroon, A.G. Radwan, FPGA implementation of a chaotic oscillator with odd/even symmetry and its application. Integration 72, 163–170 (2020)

    Google Scholar 

  45. F.J. Torres, G.V. Guerrero, C.D. García, J.F. Gomez, M. Adam, R.F. Escobar, Master–slave synchronization of robot manipulators driven by induction motors. IEEE Latin Am. Trans. 14(9), 3986–3991 (2016)

    Google Scholar 

  46. Xilinx, Vivado design suite—hlx editions (2016)

  47. X. Yu-meng, Z. Yao, A. Hobiny, J. Ma, Differential coupling contributes to synchronization via a capacitor connection between chaotic circuits. Front. Inf. Technol. Electron. Eng. 20, 571 (2019)

    Google Scholar 

  48. C.J. Zuniga-Aguilar, H.M. Romero-Ugalde, J.F. Gomez-Aguilar, R.F. Escobar-Jiménez, M. Valtierra-Rodríguez, Solving fractional differential equations of variable-order involving operators with Mittag–Leffler kernel using artificial neural networks. Chaos Solitons Fract. 103, 382–403 (2017)

    MathSciNet  MATH  Google Scholar 

  49. C.J. Zuniga-Aguilar, A. Coronel-Escamilla, J.F. Gomez-Aguilar et al., New numerical approximation for solving fractional delay differential equations of variable order using artificial neural networks. Eur. Phys. J. Plus 133, 75 (2018)

    Google Scholar 

  50. C.J. Zuniga-Aguilar, J.F. Gomez-Aguilar, R.F. Escobar-Jimenez et al., Robust control for fractional variable-order chaotic systems with non-singular kernel. Eur. Phys. J. Plus 133, 13 (2018)

    Google Scholar 

  51. C.J. Zuniga-Aguilar, J.F. Gomez-Aguilar, R.F. Escobar Jimenez, H.M. Romero Ugalde, A novel method to solve variable-order fractional delay differential equations based in Lagrange interpolations. Chaos Solitons Fract. 126, 266–282 (2019)

    MathSciNet  MATH  Google Scholar 

Download references

Funding

The research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Author information

Authors and Affiliations

  1. Department of Computer Engineering, University of Sharjah, Sharjah, United Arab Emirates

    Talal Bonny

Authors
  1. Talal Bonny
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Talal Bonny.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bonny, T. Chaotic or Hyper-chaotic Oscillator? Numerical Solution, Circuit Design, MATLAB HDL-Coder Implementation, VHDL Code, Security Analysis, and FPGA Realization. Circuits Syst Signal Process 40, 1061–1088 (2021). https://doi.org/10.1007/s00034-020-01521-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00034-020-01521-8

Keywords