Abstract
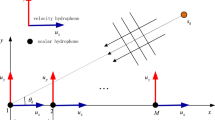
In order to generate volumetric underwater acoustic images, planar arrays are often used to collect the signals coming from a 3-D scene in underwater environment. These acquired signals are commonly processed using the 2-D conventional beamforming method. The 2-D conventional beamforming is robust and the most commonly used method. However, the 2-D conventional beamforming suffers from fat beams and high-level sidelobes. High-resolution beamforming, based on the inverse of the signal covariance matrix, such as minimum-variance distortionless response, produces narrow beamwidth and low sidelobe levels but is sensitive to signal mismatch and requires many snapshots of data. In order to overcome the above-mentioned limitations, this paper applies a 2-D deconvolution algorithm to the 2-D conventional beamforming result of planar array in order to improve the beamwidth and suppress the high-level sidelobes. The 2-D deconvolved beam power produces narrow beams, and low sidelobe levels without compromising the robustness of 2-D conventional beamforming. The 2-D deconvolution algorithm provides higher output signal-to-noise ratio than the 2-D conventional beamforming for isotropic noise. The vector extrapolation method is improved to make it applicable on two-dimensional data. The detailed implementations of the original 2-D deconvolved beamforming and the efficient 2-D deconvolved beamforming are presented. Simulations and experiments are conducted to validate the performance of the proposed method.



















Similar content being viewed by others
Data availability
Due to the data reproducing these findings also forms part of an ongoing study, so supporting data is not available.
References
D.S.C. Biggs, M. Andrews, Acceleration of iterative image restoration algorithms. Opt. Soc. Am. 36(8), 1766–1775 (1997)
D.C. Calvo, A.L. Thangawng, M. Nicholas, C.L. Layma, Thin Fresnel zone plate lenses for focusing underwater sound. Appl. Phys. Lett. 107(1), 014103 (2015)
H. Cox, R.M. Zeskind, M.H. Owen, Robust adaptive beamforming. IEEE Trans. Acoust. Speech Signal Process. 35(10), 1365–1376 (1987)
B.F. Cron, C.H. Sherman, Spatial correlation functions for various noise models. J. Acoust. Soc. Am. 34, 1732 (1962)
A.C. Dhanantwari, S. Stergiopoulos, L. Song, C. Parodi, F. Bertora, P. Pellegretti, A. Questa, An efficient 3D beamformer implementation for real-time 4D ultra sound systems deploying array probes, in IEEE Ultrasonics Symposium, August 23–27(Canada, Toronto, 2004), pp. 1421–1424
G.F. Edelmann, J.S. Rogers, S.L. Means, Beam space compressive spatial spectrum estimation on large aperture acoustic arrays. J. Acoust. Soc. Am. 136(4), 2214–2214 (2014)
P. Gersoft, A. Xenaki, C.F. Mechlenbrauker, Multiple and single snapshot compressive beamforming. J. Acoust. Soc. Am. 138(4), 2003 (2015)
J. Huang, T. Zhou, W. Du, J. Shen, W. Zhang, Smart ocean: a new fast deconvolved beamforming algorithm for multibeam sonar. Sensors 18(11), 4013 (2018)
L. Hellequin, J.M. Boucher, X. Lurton, Processing of high-frequency multibeam echo sounder data for seafloor characterization. IEEE J. Ocean. Eng. 28(1), 78–98 (2003)
L. Hellequin, Statistical characterization of multibeam echo sounder data, in IEEE OCEANS’98 Conference Proceeding, September 28–October 1 (France, Nice, 1998), pp. 228–233
M.J. Jacobson, Space-time correlation in spherical and circular noise fields. J. Acoust. Soc. Am. 34(7), 971 (1962)
X. Jiang, W. Zeng, A. Yasotharan, H.C. So, T. Kirubarajan, Robust beamforming by linear programming. IEEE Trans. Signal Process. 62(7), 1834–1849 (2014)
I. Kaiho, A dream for realization of high-speed, 3D volume image by lens-focused method, in Proceedings of the 7th Congress of the Asian Federation of Ultrasound in Medicine and Biology, May 17–21(Japan, Utsunomiya, 2004), pp. 38–46
L.B. Lucy, An iterative technique for the rectification of observed distributions. Astron. J. 79(6), 745–754 (1974)
H. Li, B. Wei, J. Zhu, C. Li, S. Xing, Calibration of multibeam echo sounder transducer array based on focused beamforming. Sens. J. IEEE. 18(24), 10199–10207 (2018)
A.P. Lyons, D.A. Abraham, Statistical characterization of high-frequency shallow-water seafloor backscatter. J. Acoust. Soc. Am. 106(3), 1307–1315 (1999)
V. Murino, A. Trucco, Dynamic focusing by FFT beamforming for underwater 3D imaging, in Proceedings of 1st International Conference on Image Processing, November 13–16 (America, Austin, 1994), pp. 169–172
B. Maranda, Efficient digital beamforming in the frequency domain. J. Acoust. Soc. Am. 86(1813), 1813–1819 (1989)
W.H. Richardson, Bayesian-based iterative method of image restoration. J. Opt. Soc. Am. 62(1), 55–59 (1972)
P. Stoica, Z. Wang, J. Li, Robust capon beamforming. IEEE Signal Process. Lett. 10(6), 172–175 (2003)
Y. Takase, T. Anada, T. Tsuchiya, N. Nakamura, Realtime sonar system using acoustic lens and numerical analysis based on 2D/3D parabolic equation method, in IEEE OCEANSE 2005 Europe, June 20–23(France, Brest, 2005), pp. 23–28.
F. Zhang, A. Bilas, A. Dhanantwari, K.N. Plataniotis, R. Abiprojo, S. Stergiopoulos, Parallelization and performances of 3D ultrasound imaging beamforming algorithms on modern clusters, in Proceedings of the 16th international conference on Supercomputing, June 22–26 (America, New York, 2002), pp. 294–304
L.J. Ziomek, Fundamentals of Acoustic Field Theory and Space-Time Signal Processing (CRC Press, Boca Raton, 1995). (ch. 7)
Acknowledgements
This work was supported by the National Natural Science Foundation of China (41976176, U1709203,52001097), the National Key R&D Program of China (2016YFC1402303, 2018YFF01013401), and the Financial Assistance from Postdoctoral Scientific Research Developmental Fund of Heilongjiang (LBH-Q18042).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Zhou, T., Huang, J., Du, W. et al. 2-D Deconvolved Conventional Beamforming for a Planar Array. Circuits Syst Signal Process 40, 5572–5593 (2021). https://doi.org/10.1007/s00034-021-01733-6
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00034-021-01733-6