Skip to main content
Springer Nature Link
Log in

The Generalized Compressed Nested Array for the Construction of Fourth-order Difference Co-array

  • Short Paper
  • Published:
Circuits, Systems, and Signal Processing Aims and scope Submit manuscript

Abstract

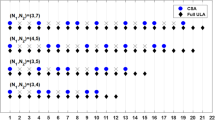
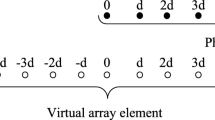
In the present study, the generalized compressed nested array (GCNA) is proposed to improve the fourth-order cumulant-based direction of arrival (DOA) estimation performance when the small-scale array is deployed. The main objective of this study is to demonstrate that the new-formed array can form the sum co-array, which is close to the nested array, by a few sensors. Meanwhile, it is found that the difference co-array of its sum co-array or the fourth-order difference co-array (FODC) of GCNA is hole-free so that it can achieve a long consecutive virtual array. Obtained results show that for less than 12 sensors, GCNA can achieve the longest consecutive virtual array when the comparison is made with conventional FODC-based sparse arrays. It is inferred that for a small-scale sensor array, the GCNA can acquire more degrees of freedom (DOFs) for DOA estimation than other sparse arrays. In order to evaluate the performance of the proposed sparse array, numerous simulations are carried out to compare the number of resolved sources and estimation accuracy of different sparse arrays. Accordingly, it is concluded that the proposed GCNA outperforms conventional representative sparse arrays.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Data availability statement

The data used to support the findings of this study are available from the corresponding author upon reasonable request.

References

  1. A. Ahmed, Y.D. Zhang, B. Himed, Effective nested array design for fourth-order cumulant-based DOA estimation. The IEEE Radar Conference 998–1002(2017)

  2. G. Birot, L. Albera, P. Chevalier, Sequential high-resolution direction finding from higher order statistics. IEEE Trans. Signal Process. 58(8), 4144–4155 (2010)

    Article  MathSciNet  Google Scholar 

  3. J. Cai, W. Liu, R. Zong, Q. Shen, An expanding and shift scheme for constructing fourth-order difference coarrays. IEEE Signal Process. Lett. 24(4), 480–484 (2017)

    Article  Google Scholar 

  4. P. Chevalier, L. Albera, A. Ferreol, P. Comon, On the virtual array concept for higher order array processing. IEEE Trans. Signal Process. 53(4), 1254–1271 (2005)

    Article  MathSciNet  Google Scholar 

  5. P. Chevalier, A. Ferreol, L. Albera, High-resolution direction finding from higher order statistics: the 2q -MUSIC algorithm. IEEE Trans. Signal Process. 54(8), 2986–2997 (2006)

    Article  Google Scholar 

  6. M.C. Dŏgan, J.M. Mendel, Applications of cumulants to array processing I: Aperture extension and array calibration. IEEE Trans. Signal Process. 43(5), 1200–1216 (1995)

    Article  Google Scholar 

  7. J. He, L. Li, T. Shu, 2-D direction finding using parallel nested arrays with full co-array aperture extension. Signal Process. 178(2021)

  8. J. He, Z. Zhang, C. Gu, T. Shu, W. Yu, Cumulant-based 2-D direction estimation using an acoustic vector sensor array. IEEE Trans. Aerosp. Electron. Syst. 56(2), 956–971 (2020)

    Article  Google Scholar 

  9. C.L. Liu, P.P. Vaidyanathan, Super nested arrays: Linear sparse arrays with reduced mutual coupling-Part I: Fundamentals. IEEE Trans. Signal Process. 64(15), 3997–4012 (2016)

    Article  MathSciNet  Google Scholar 

  10. C.L. Liu, P.P. Vaidyanathan, Super nested arrays: linear sparse arrays with reduced mutual coupling-Part II: High-order extensions. IEEE Trans. Signal Process. 64(16), 4203–4217 (2016)

    Article  MathSciNet  Google Scholar 

  11. J. Liu, Y. Zhang, Y. Lu, S. Ren, S. Cao, Augmented nested arrays with enhanced DOF and reduced mutual coupling. IEEE Trans. Signal Process. 65(21), 4203–4217 (2017)

    Article  MathSciNet  Google Scholar 

  12. J. Liang, D. Liu, Passive localization of near-field sources using cumulant. IEEE Sensors J. 9(8), 953–960 (2009)

    Article  Google Scholar 

  13. J. Liang, D. Liu, Passive localization of mixed near-field and far field sources using two-stage MUSIC algorithm. IEEE Trans. Signal Process. 58(1), 108–120 (2010)

    Article  MathSciNet  Google Scholar 

  14. J. Li, Y. Wang, L.B. Cédric, G. Wei, B. Ma, M. Sun, Z. Yu, Simplified high-order DOA and range estimation with linear antenna array. IEEE Commun. Lett. 21(1), 76–79 (2017)

    Article  Google Scholar 

  15. P. Pal, P.P. Vaidyanathan, Nested arrays in two dimensions, Part I: Geometrical considerations. IEEE Trans. Signal Process. 60(9), 4694–4705 (2012)

    Article  MathSciNet  Google Scholar 

  16. P. Pal, P.P. Vaidyanathan, Nested arrays: a novel approach to array processing with enhanced degrees of freedom. IEEE Trans. Signal Process. 58(8), 4167–4181 (2010)

    Article  MathSciNet  Google Scholar 

  17. P. Pal, P.P. Vaidyanathan, Multiple level nested array: an efficient geometry for 2qth order cumulant based array processing. IEEE Trans. Signal Process. 60(3), 1253–1269 (2012)

    Article  MathSciNet  Google Scholar 

  18. S. Ren, T. Zhu, J. Liu, Generalized design approach for fourth-order difference co-array, in IEEE International Conference on Radar (2018)

  19. R. Schmidt, Multiple emitter location and signal parameter estimation. IEEE Trans Antennas Propag. 34(3), 276–280 (1986)

    Article  Google Scholar 

  20. T. Shu, L. Li, J. He, Near-field source localization with two-level nested arrays. IEEE Commun. Lett. 24(11), 2488–2492 (2020)

    Article  Google Scholar 

  21. Q. Shen, W. Liu, W. Cui, S. Wu, Extension of nested arrays with the fourth-order difference co-array enhancement, in Proc. IEEE Int. Conf. Acoust. Speech, Signal Process. (ICASSP), 2991-2995 (2016)

  22. Q. Shen, W. Liu, W. Cui, S. Wu, P. Pal, Simplified and enhanced multiple level nested arrays exploiting high-order difference co-arrays. IEEE Trans. Signal Process. 67(13), 3502–3515 (2019)

    Article  MathSciNet  Google Scholar 

  23. C. Shi, F. Wang, M. Sellathurai, J. Zhou, S. Salou, Power minimization based robust OFDM radar waveform design for radar and communication systems in coexistence. IEEE Trans. Signal Process. 66(5), 1316–1330 (2017)

    Article  MathSciNet  Google Scholar 

  24. J. Shi, F. Wen, T. Liu, Nested MIMO radar: coarrays, tensor modeling and angle estimation, IEEE Trans. Aerosp. Electron. Syst., https://doi.org/10.1109/TAES.2020.3034012

  25. D. Van Trees, Optimum Array Processing: Part IV of Detection (Estimation and Modulation Theory. Wiley, New York, 2002)

    Book  Google Scholar 

  26. P.P. Vaidyanathan, Sparse sensing with co-prime samplers and arrays. IEEE Trans. Signal Process. 59(2), 573–586 (2011)

    Article  MathSciNet  Google Scholar 

  27. X. Wang, M. Huang, L. Wan, Joint 2D-DOD and 2D-DOA estimation for coprime EMVS-MIMO radar, Circ. Sys. Signal Process. https://doi.org/10.1007/s00034-020-01605-5

  28. M. Yang, L. Sun, X. Yuan, B. Chen, Improved nested array with hole-free DCA and more degrees of freedom. Electron. Lett. 52(25), 2068–2070 (2016)

    Article  Google Scholar 

  29. M.L. Yang, A.M. Haimovich, X. Yuan, L. Sun, B. Chen, A unified array geometry composed of multiple identical subarrays with hole-free difference coarrays for underdetermined DOA estimation. IEEE Access 2018(6), 14238–14254 (2018)

    Article  Google Scholar 

  30. H. Zhang, Z. Zheng, Robust DOA estimator under non-Gaussian noise and insufficient sample support. Circuits Syst. Signal Process. 39, 4730–4739 (2020)

    Article  Google Scholar 

  31. Y. Zhou, Y. Li, L. Wang, C. Wen, W. Nie, The compresses nested array for Uuderdetermined DOA estimation by fourth-order difference coarrays, The 45th IEEE International Conference on Acoustics, Speech and Signal Processing (Barcelona, Spain, 2020), pp. 4167–4171

Download references

Acknowledgements

This work was sponsored by National Natural Science Foundation of China under Grants 61901371, 61901372 and 51974250. This work was also supported in part by the Natural Science Basic Research Program of Shaanxi under Grants 2020JQ-600 and 2020JQ-599, and in part by the Youth Science and Technology Nova Project in Shaanxi Province under grant 2020KJXX-018.

Author information

Authors and Affiliations

  1. School of Electronics Engineering, Xi’an Shiyou University, Xi’an, 710065, China

    Bo Dang

  2. School of Information Science and Technology, Northwest University, Xi’an, 710127, China

    Yan Zhou

Authors
  1. Bo Dang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Yan Zhou
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Yan Zhou.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Dang, B., Zhou, Y. The Generalized Compressed Nested Array for the Construction of Fourth-order Difference Co-array. Circuits Syst Signal Process 40, 6340–6353 (2021). https://doi.org/10.1007/s00034-021-01769-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00034-021-01769-8

Keywords