Skip to main content
SpringerLink
Log in

DOA Estimation of Noncircular Signals Under Impulsive Noise Using a Novel Empirical Characteristic Function-Based MUSIC

  • Published:
Circuits, Systems, and Signal Processing Aims and scope Submit manuscript

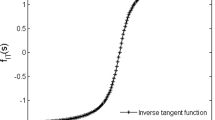
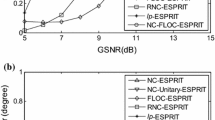
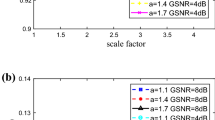
Abstract

Noncircular (NC) signals constitute a significant class of signals that are frequently employed in communication systems. In the presence of extremely impulsive noises, determining the direction of these signals can present significant challenges. When the noise tail becomes heavier or the signal-to-noise ratio decreases, existing methods yield poor results. Recently, the authors have developed an empirical characteristic function (ECF)-based MUSIC algorithm. This method is called ECF-MUSIC. Despite its robustness and high precision, it only works with circular signals. This is a direct result of the covariance matrix of the ECF-MUSIC method containing a nonzero relation matrix. In this paper, a novel ECF-based MUSIC is developed to exploit the ECF in DOA estimation of NC signals. Using the CF of the output of the extended array, a new covariance-like matrix is introduced. Then, an analysis of eigen-decomposition is performed to develop a new MUSIC algorithm. Due to the unique properties of ECF, such as its ability to preserve information, this method yields precise results, particularly in the presence of heavy tail noise. Additionally, it doubles the maximum number of detectable sources. The Monte Carlo simulations demonstrate the excellent performance of the method, NC-ECF-MUSIC. This method outperforms existing methods in terms of estimation error and resolution, as demonstrated by these results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17

Similar content being viewed by others

Data Availability Statement

The dataset generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

References

  1. M. Asghari et al., ECF-MUSIC: an empirical characteristic function based direction of arrival (DOA) estimation in the presence of impulsive noise. Digit. Signal Process. 123, 103440 (2022)

    Article  Google Scholar 

  2. S. Bayat, S. Daei, Separating radar signals from impulsive noise using atomic norm minimization. IEEE Trans. Circuits Syst. II Express Br. 68(6), 2212–2216 (2021)

    Google Scholar 

  3. H. Belkacemi, S. Marcos, Robust subspace-based algorithms for joint angle/Doppler estimation in non-Gaussian clutter. Signal Process. 87(7), 1547–1558 (2007)

    Article  MATH  Google Scholar 

  4. P. Chargé, Y. Wang, J. Saillard, A non-circular sources direction finding method using polynomial rooting. Signal Process. 81(8), 1765–1770 (2001)

    Article  MATH  Google Scholar 

  5. H. Chen et al., Efficient two-dimensional direction-of-arrival estimation for a mixture of circular and noncircular sources. IEEE Sens. J. 16(8), 2527–2536 (2016)

    Article  Google Scholar 

  6. M.A. Chitre, J.R. Potter, S. Ong, Optimal and near-optimal signal detection in snapping shrimp dominated ambient noise. IEEE J. Ocean. Eng. 31(2), 497–503 (2006)

    Article  Google Scholar 

  7. Y.-H. Choi, Simple direction finding of noncircular signals using the centro-Hermitian property. Digit. Signal Process. 106, 102847 (2020)

    Article  Google Scholar 

  8. Z. Dai et al., Computational efficient two-dimension doa estimation for incoherently distributed noncircular sources with automatic pairing. IEEE Access 5, 20249–20259 (2017)

    Article  Google Scholar 

  9. H. Gao et al., Monostatic MIMO radar direction finding in impulse noise. Digit. Signal Process. 117, 103198 (2021)

    Article  Google Scholar 

  10. P. Gounon, C. Adnet, J. Galy, Localization angulaire de signaux non circulaires. Traitement du Signal 15, 17–23 (1998)

    MATH  Google Scholar 

  11. Haardt, M. and F. Romer, Enhancements of unitary ESPRIT for non-circular sources. in 2004 IEEE International Conference on Acoustics, Speech, and Signal Processing. 2004.

  12. G. Hastie et al., Effects of impulsive noise on marine mammals: investigating range-dependent risk. Ecol. Appl. 29, e01906 (2019)

    Article  Google Scholar 

  13. Z. Huang et al., 2-D DOA estimation for incoherently distributed sources considering mixed circular and noncircular signals in massive MIMO system. IEEE Access 7, 106900–106911 (2019)

    Article  Google Scholar 

  14. Z. Jinfeng, Q. Tianshuang, A novel covariation based noncircular sources direction finding method under impulsive noise environments. Signal Process. 98, 252–262 (2014)

    Article  Google Scholar 

  15. R.J. Kozick, B.M. Sadler, Maximum-likelihood array processing in non-Gaussian noise with Gaussian mixtures. IEEE Trans. Signal Process. 48(12), 3520–3535 (2000)

    Article  MathSciNet  Google Scholar 

  16. S. Li et al., DOA estimation based on sparse representation of the fractional lower order statistics in impulsive noise. IEEE/CAA Journal of Automatica Sinica 5(4), 860–868 (2018)

    Article  MathSciNet  Google Scholar 

  17. L. Liang et al., Direction of arrival estimation with off-grid target based on sparse reconstruction in impulsive noise. J. Low Freq. Noise Vib. Act. Control 40, 315–331 (2020)

    Article  Google Scholar 

  18. D. Liu et al., A novel reduced-dimensional beamspace unitary ESPRIT algorithm for monostatic MIMO radar. Digit. Signal Process. 114, 103027 (2021)

    Article  Google Scholar 

  19. S. Luan et al., Generalized covariance-based ESPRIT-like solution to direction of arrival estimation for strictly non-circular signals under alpha-stable distributed noise. Digit. Signal Process. 118, 103214 (2021)

    Article  Google Scholar 

  20. S. Luan et al., Generalized covariance for non-Gaussian signal processing and GC-MUSIC under alpha-stable distributed noise. Digit. Signal Process. 110, 102923 (2021)

    Article  Google Scholar 

  21. N.D. Merchant et al., Impulsive noise pollution in the Northeast Atlantic: reported activity during 2015–2017. Mar. Pollut. Bull. 152, 110951 (2020)

    Article  Google Scholar 

  22. A. Naghavi et al., A sequential MUSIC algorithm for scatterers detection in SAR tomography enhanced by a robust covariance estimator. Digital Signal Process. 128, 103621 (2022)

    Article  Google Scholar 

  23. B. Picinbono, On circularity. IEEE Trans. Signal Process. 42(12), 3473–3482 (1994)

    Article  Google Scholar 

  24. P.J. Schreier, L. Scharf, Statistical Signal Processing of Complex-Valued Data- The Theory of Improper and Noncircular Signals. Statistical Signal Processing of Complex-Valued Data: The Theory of Improper and Noncircular Signals, (2010), p. 1–309.

  25. L. Shengyang et al., BNC-based projection approximation subspace tracking under impulsive noise. IET Radar Sonar Navig. 11, 1055–1061 (2017)

    Article  Google Scholar 

  26. J. Steinwandt, F. Roemer, M. Haardt, Sparsity-based direction-of-arrival estimation for strictly non-circular sources. in 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2016.

  27. J. Steinwandt et al., Sparsity-aware direction finding for strictly non-circular sources based on rank minimization. in 2016 IEEE Sensor Array and Multichannel Signal Processing Workshop (SAM). 2016.

  28. A. Swami, B. Sadler, TDE, DOA and related parameter estimation problems in impulsive noise. in Proceedings of the IEEE Signal Processing Workshop on Higher-Order Statistics, 1997.

  29. W. Tan et al., Direction-of-arrival of strictly non-circular sources based on weighted mixed-norm minimization. EURASIP Journal on Wireless Communications and Networking, 2018. 2018.

  30. Y.-N. Tian et al., Group sparse underwater acoustic channel estimation with impulsive noise: Simulation results based on Arctic ice cracking noise. J. Acoust. Soc. Am. 146(4), 2482–2491 (2019)

    Article  Google Scholar 

  31. P. Tsakalides, C.L. Nikias, The robust covariation-based MUSIC (ROC-MUSIC) algorithm for bearing estimation in impulsive noise environments. IEEE Trans. Signal Process. 44(7), 1623–1633 (1996)

    Article  Google Scholar 

  32. L. Wan et al., DOA estimation for coherently distributed sources considering circular and noncircular signals in massive MIMO systems. IEEE Syst. J. 11(1), 41–49 (2017)

    Article  Google Scholar 

  33. B. Wen, Y. Wei, Z. Lu, Sea clutter suppression and target detection algorithm of marine radar image sequence based on spatio-temporal domain joint filtering. Entropy 24, 250 (2022)

    Article  MathSciNet  Google Scholar 

  34. B. Yang et al., Direction-of-arrival estimation of strictly noncircular signal by maximum likelihood based on moving array. IEEE Commun. Lett. 23(6), 1045–1049 (2019)

    Article  Google Scholar 

  35. X. Yang et al., Central DOA estimation of incoherently distributed noncircular sources with cross-correlation matrix. Circuits Syst. Signal Process. 2015. 34.

  36. J. Yin et al., ML-based single-step estimation of the locations of strictly noncircular sources. Digit. Signal Process. 69, 224–236 (2017)

    Article  Google Scholar 

  37. J. Yu, Empirical characteristic function estimation and its applications. Economet. Rev. 23(2), 93–123 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  38. Z. Yuan et al., Characteristics of snapping shrimp noise in the northeastern East China Sea. J. Acoust. Soc. Am. 141(5), 3525–3526 (2017)

    Article  Google Scholar 

  39. W. Zeng, H.C. So, L. Huang, lp-MUSIC: robust direction-of-arrival estimator for impulsive noise environments. IEEE Trans. Signal Process. 61(17), 4296–4308 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  40. D. Zha, T. Qiu, Direction finding in non-Gaussian impulsive noise environments. Digit. Signal Process. 17, 451–465 (2007)

    Article  Google Scholar 

  41. J. Zhang, T. Qiu, The fractional lower order moments based ESPRIT algorithm for noncircular signals in impulsive noise environments. Wirel. Pers. Commun. 96(2), 1673–1690 (2017)

    Article  Google Scholar 

  42. J. Zhang, T. Qiu, S. Luan, An efficient real-valued sparse Bayesian learning for non-circular signal’s DOA estimation in the presence of impulsive noise. Digital Signal Process. 106, 102838 (2020)

    Article  Google Scholar 

  43. J. Zhang et al., Bounded non-linear covariance based ESPRIT method for noncircular signals in presence of impulsive noise. Digit. Signal Process. 87, 104–111 (2019)

    Article  Google Scholar 

  44. J. Zhang et al., A novel correntropy based DOA estimation algorithm in impulsive noise environments. Signal Process. 104, 346–357 (2014)

    Article  Google Scholar 

  45. X. Zhang et al., DOA Estimation of mixed circular and noncircular sources using nonuniform linear array. IEEE Transactions on Aerospace and Electronic Systems, (2022), p. 1–1.

  46. A. Zoubir, P. Chargé, Y. Wang, Non circular sources localization with ESPRIT. in Proc. European Conference on Wireless Technology (ECWT 2003). 2003.

Download references

Author information

Authors and Affiliations

  1. Mechanical Engineering Department, Amirkabir University of Technology, Tehran, Iran

    Mohsen Asghari & Seyed Mehdi Rezaei

  2. New Technologies Research Center, Amirkabir University of Technology, Tehran, Iran

    Mohammad Zareinejad

  3. Electrical Engineering Department, Amirkabir University of Technology, Tehran, Iran

    Hamidreza Amindavar

Authors
  1. Mohsen Asghari
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mohammad Zareinejad
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Seyed Mehdi Rezaei
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Hamidreza Amindavar
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mohammad Zareinejad.

Ethics declarations

Conflict of interest

No funding was received to assist with the preparation of this manuscript.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Asghari, M., Zareinejad, M., Rezaei, S.M. et al. DOA Estimation of Noncircular Signals Under Impulsive Noise Using a Novel Empirical Characteristic Function-Based MUSIC. Circuits Syst Signal Process 42, 3706–3743 (2023). https://doi.org/10.1007/s00034-022-02289-9

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00034-022-02289-9

Keywords

Search

Navigation