Skip to main content
SpringerLink
Log in

IF Estimation of Multicomponent Nonstationary Signals Based on AFSST

  • Published:
Circuits, Systems, and Signal Processing Aims and scope Submit manuscript

Abstract

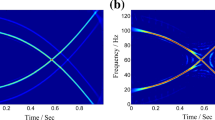
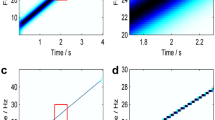
The instantaneous frequency (IF) provides important characteristic information for analyzing signals. To improve the accuracy of IF estimation, time–frequency (TF) analysis with high resolution and high aggregation is necessary. A new IF estimation method is proposed in this paper, which is referred to as ridge path regrouping based on an adaptive short-time Fourier high-order synchrosqueezing transform (AFSST). In the TF analysis of the non-stationary signal, we optimize the window function of the short-time Fourier transform to be adaptive to signal characteristics, and then perform the high-order synchrosqueezing transform. Based on the high-resolution time–frequency distribution (TFD), the frequency ridge of the signal is extracted, and the ridge of the modal aliasing at the intersection is discarded and reorganized according to the fundamentals. Experiments on multicomponent nonstationary signals were performed, and the results show that AFSST has satisfactory TF aggregation and TF resolution. IF estimation experiment based on AFSST, the results indicate that the proposed method can estimate the IF accurately even under a low signal-to-noise ratio (SNR).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. J. Akram, N.A. Khan, S. Ali, Multi-component instantaneous frequency estimation using signal decomposition and time-frequency filtering. SIViP 14, 1663–1670 (2020). https://doi.org/10.1007/s11760-020-01711-6

    Article  Google Scholar 

  2. S. Ali, N.A. Khan, X. Luo, Blind source separation schemes for mono-sensor and multi-sensor systems with application to signal detection. Circuits Syst. Signal Process. 36, 4615–4636 (2017). https://doi.org/10.1007/s00034-017-0533-6

    Article  MathSciNet  Google Scholar 

  3. S.M. Beeraka, A. Kumar, M. Sameer, Accuracy enhancement of epileptic seizure detection: a deep learning approach with hardware realization of STFT. Circuits Syst. Signal Process. 41, 461–484 (2022). https://doi.org/10.1007/s00034-021-01789-4

    Article  Google Scholar 

  4. B. Boashash, P.J. Black, An efficient real-time implementation of the Wigner-Ville distribution. IEEE Trans. Acoust. Speech Signal Process. 35(11), 1611–1618 (1987). https://doi.org/10.1109/TASSP.1987.1165070

    Article  Google Scholar 

  5. B. Boashash, Estimating and interpreting the instantaneous frequency of a signal-Part 1: fundamentals. IEEE Proc. 80(4), 520–538 (1992). https://doi.org/10.1109/5.135376

    Article  Google Scholar 

  6. B. Boashash, Estimating and interpreting the instantaneous frequency of a signal-Part 2: algorithms and applications. IEEE Proc. 80, 540–568 (1992). https://doi.org/10.1109/5.135378

    Article  Google Scholar 

  7. V. Bruni, M. Tartaglione, D. Vitulano, A pde-based analysis of the spectrogram image for instantaneous frequency estimation. Mathematics 9(3), 247 (2021). https://doi.org/10.3390/math9030247

    Article  Google Scholar 

  8. S. Chen, X. Dong, G. Xing, Z.K. Peng, W.M. Zhang, G. Meng, Separation of overlapped non-stationary signals by ridge path regrouping and intrinsic chirp component decomposition. IEEE Sens. J. 17(18), 5994–6005 (2017). https://doi.org/10.1109/JSEN.2017.2737467

    Article  Google Scholar 

  9. I. Daubechies, J. Lu, H.T. Wu, Synchrosqueezed wavelet transforms: an empirical mode decomposition-like tool. Appl. Comput. Harmon Anal. 30(2), 243–261 (2011). https://doi.org/10.1016/j.acha.2010.08.002

    Article  MathSciNet  MATH  Google Scholar 

  10. I. Daubechies, S. Maes, A Nonlinear Squeezing of the Continuous Wavelet Transform Based on Auditory Nerve Models, in Wavelets in Medicine and Biology. ed. by A. Aldroubi, M. Unser (CRC Press, London, 1996), pp.527–546. https://doi.org/10.1201/9780203734032-20

    Chapter  Google Scholar 

  11. I. Djurovic, L.J. Stankovic, An algorithm for the Wigner distribution based instantaneous frequency estimation in a high noise environment. Signal Process. 84(4), 631–643 (2004). https://doi.org/10.1016/j.sigpro.2003.12.006

    Article  MATH  Google Scholar 

  12. I. Djurovic, QML-RANSAC instantaneous frequency estimator for overlapping multicomponent signals in the time-frequency plane. IEEE Signal Process. Lett. 25(3), 447–451 (2018). https://doi.org/10.1109/LSP.2018.2795554

    Article  Google Scholar 

  13. I. Djurovic, RANSAC algorithm for instantaneous frequency estimation and reconstruction of frequency-modulated undersampled signals. EURASIP J. Adv. Signal Process. 2021, 19 (2021). https://doi.org/10.1186/s13634-021-00726-6

    Article  Google Scholar 

  14. H.U. Zhong-Lai, Z.H. Jian-Zhong, Z.O. Zhi-Hui, A second-order synchrosqueezing S-transform and its application in seismic spectral decomposition. Chin. J. Geophys. 60, 2833–2844 (2017). https://doi.org/10.6038/cjg20170728

    Article  Google Scholar 

  15. L. Jiang, L. Li, G.Q. Zhao, Y. Pan, Instantaneous frequency estimation of nonlinear frequency-modulated signal under strong noise environment. Circuits Syst. Signal Process. 35, 3734–3744 (2016). https://doi.org/10.1007/s00034-015-0230-2

    Article  MathSciNet  Google Scholar 

  16. Q.T. Jiang, B.W. Suter, Instantaneous frequency estimation based on synchrosqueezing wavelet transform. Signal Process. 138, 167–181 (2017). https://doi.org/10.1016/j.sigpro.2017.03.007

    Article  Google Scholar 

  17. N.A. Khan, S. Ali, A robust and efficient instantaneous frequency estimator of multi-component signals with intersecting time-frequency signatures. Signal Process. 177, 107728 (2020). https://doi.org/10.1016/j.sigpro.2020.107728

    Article  Google Scholar 

  18. N.A. Khan, M. Mohammadi, I. Stankovic, Sparse reconstruction based on iterative TF domain filtering and Viterbi based if estimation algorithm. Signal Process. 166, 107260 (2020). https://doi.org/10.1016/j.sigpro.2019.107260. (ISSN 0165-1684)

    Article  Google Scholar 

  19. N.A. Khan, M. Mohammadi, Detection of frequency modulated signals using a robust if estimation algorithm. Circuits Syst Signal Process. 39(4), 2223–2231 (2020). https://doi.org/10.1007/s00034-019-01258-z

    Article  MATH  Google Scholar 

  20. L. Li, H.Y. Cai, H.X. Han, Q.T. Jiang, H.B. Ji, Adaptive short-time Fourier transform and synchrosqueezing transform for non-stationary signal separation. Signal Process. 166, 10723 (2020). https://doi.org/10.1016/j.sigpro.2019.07.024

    Article  Google Scholar 

  21. L. Li, H.Y. Cai, Q.T. Jiang, Adaptive synchrosqueezing transform with a time-varying parameter for non-stationary signal separation. Appl. Comput. Harmon. Anal. 49(3), 1075–1106 (2020). https://doi.org/10.1016/j.acha.2019.06.002

    Article  MathSciNet  MATH  Google Scholar 

  22. P. Li, Q.H. Zhang, IF estimation of overlapped multicomponent signals based on viterbi algorithm. Circuits Syst. Signal Process. 39, 3105–3124 (2020). https://doi.org/10.1007/s00034-019-01314-8

    Article  Google Scholar 

  23. T. Oberlin, S. Meignen, V. Perrier, The Fourier-based synchrosqueezing transform. ICASSP. in IEEE International Conference on Acoustics, Speech and Signal Processing. Florence, Italy, pp. 315–319 (2014). https://doi.org/10.1109/ICASSP.2014.6853609

  24. D.A. Okaya, E. Karaeorgi, T.V. McEvilly, P.E. Malin, Removing vibrator-induced correlation artifacts by filtering in frequency-uncorrelated time space. Geophysics 57(7), 916–926 (1992). https://doi.org/10.1190/1.1443304

    Article  Google Scholar 

  25. D.H. Pham, S. Meignen, High-order synchrosqueezing transform for multicomponent signals analysis-with an application to gravitational-wave signal. IEEE Trans. Signal Process. 65, 3168–3178 (2017). https://doi.org/10.1109/TSP.2017.2686355

    Article  MathSciNet  MATH  Google Scholar 

  26. E. Sejdic, I. Djurovic, L. Stankovic, Quantitative performance analysis of scalogram as instantaneous frequency estimator. IEEE Trans. Signal Process. 56(8), 3837–3845 (2008). https://doi.org/10.1109/TSP.2008.924856

    Article  MathSciNet  MATH  Google Scholar 

  27. S. Sinha, P.S. Routh, P.D. Anno, J.P. Castagna, Spectral decomposition of seismic data with continuous-wavelet transform. Geophysics 70(6), 19–25 (2005). https://doi.org/10.1190/1.2127113

    Article  Google Scholar 

  28. L. Stankovic, I. Djurovic, S. Stankovic, M. Simeunovic, S. Djukanovic, M. Dakovic, Instantaneous frequency in time-frequency analysis: enhanced concepts and performance of estimation algorithms. Digit. Signal Process. 2, 1–13 (2014). https://doi.org/10.1016/j.dsp.2014.09.008

    Article  Google Scholar 

  29. X.F. Su, R. Xiao, M.Z. Zhu, Method for IF estimation of multicomponent FM signals. J. Xid. Univ. 46(1), 51–56 (2019). https://doi.org/10.19665/j.issn1001-2400.2019.01.009

    Article  Google Scholar 

  30. X.X. Zheng, Y.B. Wei, J. Liu, H.S. Jiang, Multi-synchrosqueezing S-transform for fault diagnosis in rolling bearings. Meas. Sci. Technol. 32, 025013 (2021). https://doi.org/10.1088/1361-6501/abb620

    Article  Google Scholar 

  31. P. Zhou, Y. Yang, S. Chen, Parameterized model based blind intrinsic chirp source separation. Digit. Signal Process. 83, 73–82 (2018). https://doi.org/10.1016/j.dsp.2018.08.015

    Article  Google Scholar 

Download references

Acknowledgements

This research was funded by the National Natural Science Foundation of China under Grant 61803294 and Natural Science Basic Research Program of Shaanxi (Program No. 2020JQ-684).

Funding

National Natural Science Foundation of China, 61803294, Li Jiang, Natural Science Foundation of Shaanxi Province, 2020JQ-684, Li Jiang.

Author information

Authors and Affiliations

  1. College of Information and Control Engineering, Xi’an University of Architecture and Technology, Xi’an, 710055, China

    Li Jiang, Wenqing Shang, Shizhao Xiang, Yudong Jiao, Yanni Wang & Junni Zhou

Authors
  1. Li Jiang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Wenqing Shang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Shizhao Xiang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Yudong Jiao
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Yanni Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Junni Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Wenqing Shang.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Ethical Approval

This article does not contain any studies with human participants or animals performed by any of the authors.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix A

Appendix A

First, we donate

$$ \begin{gathered} \tilde{\omega }(t,f) = X_{N} (t,f)R_{N} (t)^{T} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \left[ {1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} x_{2,1} (t,f){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ...{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} x_{N,1} (t,f)} \right]\left[ {r_{1} (t){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} r_{2} (t){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ...{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} r_{N} (t)} \right]^{T} \hfill \\ \end{gathered} $$
(48)
$$ y_{1} = X_{N} R_{N}^{T} $$
(49)

Then, we obtain the new equations:

$$ \left[ \begin{gathered} y_{1} \hfill \\ y_{2} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \vdots \hfill \\ y_{N - 1} \hfill \\ y_{N} \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} \begin{array}{*{20}c} 1 \\ 0 \\ \vdots \\ 0 \\ \end{array} \hfill \\ 0 \hfill \\ \end{gathered} \right.{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}c} {x_{2,1} } \\ 1 \\ \vdots \\ \begin{gathered} 0 \hfill \\ 0 \hfill \\ \end{gathered} \\ \end{array} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}c} {x_{3,1} } \\ {x_{3,2} } \\ \ddots \\ \begin{gathered} 0 \hfill \\ 0 \hfill \\ \end{gathered} \\ \end{array} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}c} \cdots \\ \cdots \\ \vdots \\ \begin{gathered} \cdots \hfill \\ \cdots \hfill \\ \end{gathered} \\ \end{array} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. \begin{gathered} x_{N,1} \hfill \\ x_{N,2} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \vdots \hfill \\ x_{N,N - 1} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1 \hfill \\ \end{gathered} \right]{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ \begin{gathered} r_{1} \hfill \\ r_{2} \hfill \\ {\kern 1pt} {\kern 1pt} \vdots \hfill \\ r_{N - 1} \hfill \\ r_{N} \hfill \\ \end{gathered} \right] $$
(50)

When N = 4,

$$ \begin{gathered} x_{k,1} = \frac{{Z_{{\alpha_{opt} }}^{{t^{k - 1} g}} }}{{Z_{{\alpha_{opt} }}^{g} }},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{for}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} k = 1...4, \hfill \\ x_{k,2} = \frac{{\partial_{f} x_{k,1} }}{{\partial_{f} x_{2,1} }} = \frac{{Z_{{\alpha_{opt} }}^{g} Z_{{\alpha_{opt} }}^{{t^{k} g}} - Z_{{\alpha_{opt} }}^{tg} Z_{{\alpha_{opt} }}^{{t^{k - 1} g}} }}{{Z_{{\alpha_{opt} }}^{g} Z_{{\alpha_{opt} }}^{{t^{2} g}} - (Z_{{\alpha_{opt} }}^{tg} )^{2} }} = \frac{{X_{k,2} }}{{X_{2,2} }} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{for}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} k = 2,3,4, \hfill \\ x_{k,3} = \frac{{\partial_{f} x_{k,2} }}{{\partial_{f} x_{3,2} }} = \frac{{X_{k + 1,3} X_{2,2} - X_{k,2} X_{3,3} }}{{X_{4,3} X_{2,2} - X_{3,2} X_{3,3} }} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{for}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} k = 3,4, \hfill \\ x_{k,4} = 1,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{for}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} k = 4, \hfill \\ \end{gathered} $$

where \(X_{k,j} = Z_{{\alpha_{opt} }}^{g} Z_{{\alpha_{opt} }}^{{t^{k} g}} - Z_{{\alpha_{opt} }}^{{t^{j - 1} g}} Z_{{\alpha_{opt} }}^{{t^{k - j + 1} g}} \;{\text{and}}\;\partial_{f} X_{k,j} = X_{k + 1,j} + X_{k + 1,j - 1} - X_{k + 1,2} .\)

Therefore, we can get

$$ \begin{aligned} y_{1} &= \tilde{\omega }_{f} = f - \frac{1}{i2\pi }\frac{{Z_{{\alpha_{opt} }}^{{g^{\prime}}} }}{{Z_{{\alpha_{opt} }}^{g} }} \\ y_{2} &= \frac{{\partial_{f} y_{1} }}{{\partial_{f} x_{2,1} }} = \frac{1}{i2\pi }\frac{{(Z_{{\alpha_{opt} }}^{g} )^{2} + Z_{{\alpha_{opt} }}^{g} Z_{{\alpha_{opt} }}^{{tg^{\prime}}} - Z_{{\alpha_{opt} }}^{tg} Z_{{\alpha_{opt} }}^{{g^{\prime}}} }}{{Z_{{\alpha_{opt} }}^{g} Z_{{\alpha_{opt} }}^{{t^{2} g}} - (Z_{{\alpha_{opt} }}^{tg} )^{2} }} = \frac{{W_{2} }}{{X_{2,2} }} \\ {\text{where, }}W_{2} &= \frac{{(Z_{{\alpha_{opt} }}^{g} )^{2} + Z_{{\alpha_{opt} }}^{g} Z_{{\alpha_{opt} }}^{{tg^{\prime}}} - Z_{{\alpha_{opt} }}^{tg} Z_{{\alpha_{opt} }}^{{g^{\prime}}} }}{i2\pi } \\ y_{3} &= \frac{{\partial_{f} y_{2} }}{{\partial_{f} x_{3,2} }} = \frac{{W_{3} X_{2,2} - W_{2} X_{3,3} }}{{X_{4,3} X_{2,2} - X_{3,2} X_{3,3} }} \\ {\text{where, }}W_{3} &= \partial_{f} W_{2} \\ y_{4} &= \frac{{\partial_{f} y_{3} }}{{\partial_{f} x_{4,3} }} \\ & = \frac{\begin{gathered} (X_{4,3} X_{2,2} - X_{3,2} X_{3,3} )W_{4} \hfill \\ - (W_{3} X_{2,2} - W_{2} X_{3,3} )(X_{5,4} + X_{5,3} - X_{5,2} ) \hfill \\ + (W_{3} X_{3,2} - W_{2} X_{4,3} )(X_{4,4} + X_{4,3} - X_{4,2} ) \hfill \\ \end{gathered} }{\begin{gathered} (X_{4,3} X_{2,2} - X_{3,2} X_{3,3} )(X_{6,4} + X_{6,3} - X_{6,2} ) \hfill \\ - (X_{5,3} X_{2,2} - X_{4,2} X_{3,3} )(X_{5,4} + X_{5,3} - X_{5,2} ) \hfill \\ + (X_{5,3} X_{3,2} - X_{4,2} X_{4,3} )(X_{4,4} + X_{4,3} - X_{4,2} ) \hfill \\ \end{gathered} } \\ {\text{where, }}W_{4} &= \partial_{f} W_{3} . \end{aligned} $$
(51)

With the help of the back-substitution algorithm, the modulation operators are calculated as:

$$ \begin{gathered} \tilde{q}^{[4,4]} = \frac{\begin{gathered} (X_{4,3} X_{2,2} - X_{3,2} X_{3,3} )W_{4} \hfill \\ - (W_{3} X_{2,2} - W_{2} X_{3,3} )(X_{5,4} + X_{5,3} - X_{5,2} ) \hfill \\ + (W_{3} X_{3,2} - W_{2} X_{4,3} )(X_{4,4} + X_{4,3} - X_{4,2} ) \hfill \\ \end{gathered} }{\begin{gathered} (X_{4,3} X_{2,2} - X_{3,2} X_{3,3} )(X_{6,4} + X_{6,3} - X_{6,2} ) \hfill \\ - (X_{5,3} X_{2,2} - X_{4,2} X_{3,3} )(X_{5,4} + X_{5,3} - X_{5,2} ) \hfill \\ + (X_{5,3} X_{3,2} - X_{4,2} X_{4,3} )(X_{4,4} + X_{4,3} - X_{4,2} ) \hfill \\ \end{gathered} } \hfill \\ \tilde{q}^{[3,4]} { = }\frac{{W_{3} X_{2,2} - W_{2} X_{3,3} }}{{X_{4,3} X_{2,2} - X_{3,2} X_{3,3} }} - \tilde{q}^{[4,4]} \frac{{X_{5,3} X_{2,2} - X_{4,2} X_{3,3} }}{{X_{4,3} X_{2,2} - X_{3,2} X_{3,3} }} \hfill \\ \tilde{q}^{[2,4]} = \frac{{W_{2} }}{{X_{2,2} }} - \tilde{q}^{[3,4]} \frac{{X_{3,2} }}{{X_{2,2} }} - \tilde{q}^{[4,4]} \frac{{X_{4,2} }}{{X_{2,2} }} \hfill \\ \end{gathered} $$
(52)

Finally, we could use \(G_{k}\) and \(G_{j,k}\) to express (52):

$$ \begin{gathered} \tilde{q}^{[4,4]} { = }G_{4} \left( {Z_{{\alpha_{opt} }}^{{t^{0...6} g}} {,}Z_{{\alpha_{opt} }}^{{t^{0...3} g^{\prime}}} } \right){,} \hfill \\ \tilde{q}^{[3,4]} { = }G_{3} \left( {Z_{{\alpha_{opt} }}^{{t^{0...4} g}} {,}Z_{{\alpha_{opt} }}^{{t^{0...2} g^{\prime}}} } \right) - \tilde{q}^{[4,4]} G_{3,4} \left( {Z_{{\alpha_{opt} }}^{{t^{0...5} g}} } \right), \hfill \\ \tilde{q}^{[2,4]} { = }G_{3} \left( {Z_{{\alpha_{opt} }}^{{t^{0...2} g}} {,}Z_{{\alpha_{opt} }}^{{t^{0...1} g^{\prime}}} } \right) - \tilde{q}^{[3,4]} G_{2,3} \left( {Z_{{\alpha_{opt} }}^{{t^{0...3} g}} } \right) - \tilde{q}^{[4,4]} G_{2,4} \left( {Z_{{\alpha_{opt} }}^{{t^{0...4} g}} } \right), \hfill \\ \end{gathered} $$
(53)

where \(G_{k} {(}Z_{{\alpha_{opt} }}^{{t^{0...m} g}} {,}Z_{{\alpha_{opt} }}^{{t^{0...m} g^{\prime}}} {)}\) is a function of \(Z_{{\alpha_{opt} }}^{{t^{l} g}}\) for \(l = 0,...,m\), and \(Z_{{\alpha_{opt} }}^{{t^{l} g^{\prime}}} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{for}}{\kern 1pt} {\kern 1pt} {\kern 1pt} l = 0,...,n.\)

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jiang, L., Shang, W., Xiang, S. et al. IF Estimation of Multicomponent Nonstationary Signals Based on AFSST. Circuits Syst Signal Process 42, 6116–6135 (2023). https://doi.org/10.1007/s00034-023-02388-1

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00034-023-02388-1

Keywords

Search

Navigation