Skip to main content
Springer Nature Link
Log in

An Unambiguous 2D DOA Estimation Algorithm by a Large-Space L-Shaped Array

  • Published:
Circuits, Systems, and Signal Processing Aims and scope Submit manuscript

Abstract

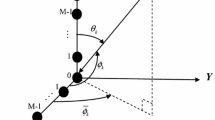
In this paper, an unambiguous two-dimensional (2D) direction of arrival (DOA) estimation algorithm based on a large-space L-shaped array is proposed. The proposed L-shaped array is composed of two large-space linear arrays. Each linear array consists of two uniform linear arrays with internal element spacing being larger than half wavelength of incident signal. Firstly, an unambiguous modified estimation of signal parameter via rotational invariance techniques (ESPRIT) algorithm is proposed to estimate the elevation angles. Then, using the estimated elevation angles, automatically matched azimuth angles can be estimated. On account of the adjustable element spacing, the proposed array is robust to mutual coupling effect. Moreover, simulation results can prove that the proposed algorithm has higher estimation accuracy than many similar 2D DOA estimation algorithms based on L-shaped array.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17

Similar content being viewed by others

Code Availability

The codes used to perform simulation experiments are available from the authors.

References

  1. J. Chen, S. Wang, X. Wei, New method for estimating two-dimensional direction of arrival based on l-shape array. J. Jilin Univ. 36(4), 590–593 (2006)

    Google Scholar 

  2. X. Dai, X. Zhang, Y. Wang, Extended DOA-matrix method for DOA estimation via two parallel linear arrays. IEEE Commun. Lett. 23(11), 1981–1984 (2019)

    Article  Google Scholar 

  3. X. Gao, X. Hao, P. Li et al., An improved two-dimensional direction-of-arrival estimation algorithm for l-shaped nested arrays with small sample sizes. Sensors 19(9), 2176 (2019)

    Article  Google Scholar 

  4. J.F. Gu, P. Wei, Joint SVD of two cross-correlation matrices to achieve automatic pairing in 2-D angle estimation problems. IEEE Antennas Wirel. Propag. Lett. 6, 553–556 (2007)

    Article  Google Scholar 

  5. H. Huang, B. Liao, X. Wang et al., A new nested array configuration with increased degrees of freedom. IEEE Access 6, 1490–1497 (2017)

    Article  Google Scholar 

  6. Y. Iizuka, K. Ichige, Extension of nested array for large aperture and high degree of freedom. IEICE Commun. Express 6(6), 381–386 (2017)

    Article  Google Scholar 

  7. S. Kikuchi, H. Tsuji, A. Sano, Pair-matching method for estimating 2-D angle of arrival with a cross-correlation matrix. IEEE Antennas Wirel. Propag. Lett. 5, 35–40 (2006)

    Article  Google Scholar 

  8. J. Li, D. Jiang, Joint elevation and azimuth angles estimation for l-shaped array. IEEE Antennas Wirel. Propag. Lett. 16, 453–456 (2016)

    Article  Google Scholar 

  9. J. Li, X. Zhang, H. Chen, Improved two-dimensional DOA estimation algorithm for two-parallel uniform linear arrays using propagator method. Signal Process. 92(12), 3032–3038 (2012)

    Article  Google Scholar 

  10. J. Liu, Y. Zhang, Y. Lu et al., Augmented nested arrays with enhanced DOF and reduced mutual coupling. IEEE Trans. Signal Process. 65(21), 5549–5563 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  11. Q. Liu, X. Yi, L. Jin et al., Two dimensional direction of arrival estimation for co-prime l-shaped array using sparse reconstruction, in 2015 8th International Congress on Image and Signal Processing (CISP) (IEEE, 2015), pp. 1499–1503

  12. S. Liu, L. Yang, D. Li et al., Subspace extension algorithm for 2D DOA estimation with l-shaped sparse array. Multidimens. Syst. Signal Process. 28(1), 315–327 (2017)

    Article  MATH  Google Scholar 

  13. S. Liu, L. Yang, D. Li et al., 2D DOA estimation for noncircular sources using l-shaped sparse array. Multidimens. Syst. Signal Process. 29(2), 489–502 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  14. S. Liu, Z. Mao, Y.D. Zhang et al., Rank minimization-based Toeplitz reconstruction for DOA estimation using coprime array. IEEE Commun. Lett. 25(7), 2265–2269 (2021)

    Article  Google Scholar 

  15. S. Liu, J. Zhao, Y. Zhang et al., 2D DOA estimation algorithm by nested acoustic vector-sensor array. Circuits Syst. Signal Process. 41(2), 1115–1130 (2022)

    Article  Google Scholar 

  16. S. Liu, J. Zhao, D. Wu et al., 2D DOA estimation of coherent signals with a separated linear acoustic vector-sensor array. China Commun. (in press) (2023)

  17. S. Marcos, A. Marsal, M. Benidir, The propagator method for source bearing estimation. Signal Process. 42(2), 121–138 (1995)

    Article  Google Scholar 

  18. G.S. Moghadam, A.B. Shirazi, Direction of arrival (DOA) estimation with extended optimum co-prime sensor array (EOCSA). Multidimens. Syst. Signal Process. 33(1), 17–37 (2022)

    Article  Google Scholar 

  19. X. Nie, L. Li, A computationally efficient subspace algorithm for 2-D DOA estimation with l-shaped array. IEEE Signal Process. Lett. 21(8), 971–974 (2014)

    Article  Google Scholar 

  20. C. Niu, Y. Zhang, J. Guo, Interlaced double-precision 2-D angle estimation algorithm using l-shaped nested arrays. IEEE Signal Process. Lett. 23(4), 522–526 (2016)

    Article  Google Scholar 

  21. P. Pal, P.P. Vaidyanathan, Nested arrays: a novel approach to array processing with enhanced degrees of freedom. IEEE Trans. Signal Process. 58(8), 4167–4181 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  22. M. Pan, P. Liu, S. Liu et al., Efficient joint DOA and TOA estimation for indoor positioning with 5G picocell base stations. IEEE Trans. Instrum. Meas. 71, 1–19 (2022)

    Google Scholar 

  23. P. Raiguru, A.K. Sahu, A. Gouda et al., Hole-free DCA for augmented co-prime array. Circuits Syst. Signal Process. 41(5), 2977–2987 (2022)

    Article  Google Scholar 

  24. R. Roy, T. Kailath, Esprit-estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process. 37(7), 984–995 (1989)

    Article  MATH  Google Scholar 

  25. R. Schmidt, Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 34(3), 276–280 (1986)

    Article  MathSciNet  Google Scholar 

  26. X. Sha, G. Cui, Direction-finding using co-prime array under impulsive noise. Math. Probl. Eng. 2022 (2022)

  27. P. Stoica, A. Nehorai, Performance study of conditional and unconditional direction-of-arrival estimation. IEEE Trans. Acoust. Speech Signal Process. 38(10), 1783–1795 (1990)

    Article  MATH  Google Scholar 

  28. W. Tang, H. Jiang, Q. Zhang, Coarray interpolation for joint DOD and DOA estimation in bistatic coprime MIMO radar via decoupled atomic norm minimization. Multidimens. Syst. Signal Process. 1–20 (2022)

  29. G. Wang, J. Xin, N. Zheng, Computationally efficient subspace-based method for two-dimensional direction estimation with l-shaped array. IEEE Trans. Signal Process. 59(7), 3197–3212 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  30. L. Yang, S. Liu, D. Li et al., Fast 2D DOA estimation algorithm by an array manifold matching method with parallel linear arrays. Sensors 16(3), 274 (2016)

    Article  Google Scholar 

  31. M. Yang, L. Sun, X. Yuan et al., Improved nested array with hole-free DCA and more degrees of freedom. Electron. Lett. 52(25), 2068–2070 (2016)

    Article  Google Scholar 

  32. Y. Yang, X. Mao, Y. Hou et al., 2-D DOA estimation via correlation matrix reconstruction for nested l-shaped array. Digit. Signal Process. 98(102), 623 (2020)

    Google Scholar 

  33. L. Zhang, S. Wu, G. Peng et al., Improved eigenstructure-based 2D DOA estimation approaches based on nyström approximation. China Commun. 16(1), 139–147 (2019)

    Google Scholar 

  34. X. Zhang, X. Gao, W. Chen et al., Improved blind 2D-direction of arrival estimation with l-shaped array using shift invariance property. J. Electromagn. Waves Appl. 23(5–6), 593–606 (2009)

    Article  Google Scholar 

  35. Y. Zhang, S. Liu, Z. Mao et al., DOA estimation based on accelerated structured alternating projection using coprime array, in Seventh Asia Pacific Conference on Optics Manufacture and 2021 International Forum of Young Scientists on Advanced Optical Manufacturing (APCOM and YSAOM 2021), vol 12166 (SPIE, 2021), pp. 196–204

Download references

Funding

This work was supported by the National Natural Science Foundation of China (62261047, 62066040), the Science and Technology Foundation of Guizhou Province of China (ZK[2022]557, [2020]1Y004), the Natural Science Foundation of Chongqing (cstc2021jcyj-bsh0198) and Tongren science and technology planning project ([2022]59) and Guizhou Provincial Education Department Youth Science and Technology Talent Development Project(KY[2019]177).

Author information

Author notes

  1. Zhao Jing contributed equally to this work.

Authors and Affiliations

  1. School of Data Science, Tongren University, 238 Qihang Road, Tongren, 554300, Guizhou, China

    Liu Sheng, Zhao Jing, Huang Yiwang & Xia Linli

  2. School of Automation, Chongqing University of Posts and Telecommunications, Chongqing, 400065, Chongqing, China

    Wu Decheng

Authors
  1. Liu Sheng
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Zhao Jing
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Wu Decheng
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Huang Yiwang
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Xia Linli
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding authors

Correspondence to Zhao Jing or Wu Decheng.

Ethics declarations

Conflict of interest

The authors declare that there is no conflict of interest regarding the publication of this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sheng, L., Jing, Z., Decheng, W. et al. An Unambiguous 2D DOA Estimation Algorithm by a Large-Space L-Shaped Array. Circuits Syst Signal Process 42, 6614–6635 (2023). https://doi.org/10.1007/s00034-023-02405-3

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00034-023-02405-3

Keywords