Skip to main content
SpringerLink
Log in

Spline Adaptive Filtering Algorithm-based Generalized Maximum Correntropy and its Application to Nonlinear Active Noise Control

  • Published:
Circuits, Systems, and Signal Processing Aims and scope Submit manuscript

Abstract

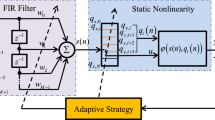
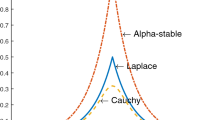
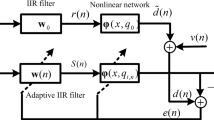
This study proposes a spline filtering algorithm-based generalized maximum correntropy criterion (GMCC), named the spline adaptive filter (SAF-)-GMCC algorithm. Compared with traditional spline algorithms, the SAF-GMCC can cope with impulsive interference effectively, because the GMCC has a low sensitivity to mutation signals. The GMCC-based variable step-size spline filtering algorithm (SAF-GMCC) is proposed to solve the limitation of the fixed step-size on the SAF-GMCC algorithm’s performance and to improve the convergence rate and steady-state error performance. Combining these algorithms with the active noise control (ANC) model, this study proposes the filtered-c generalized maximum correntropy criterion (FcGMCC) and variable step-size filtered-c generalized maximum correntropy criterion (FcVGMCC) algorithms. Finally, the nonlinear system identification model simulates an experimental environment with impulsive interference. The SAF-GMCC and SAF-VGMCC algorithms offer better robustness than the existing algorithms. And the alpha-stable noise environment simulation with different impact strengths, in the ANC model verifies the FcGMCC and FcVGMCC algorithms’ robustness in nonlinear and non-Gaussian noise environments.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Data Availability

The data that support the findings of this study are available from the corresponding author on request.

References

  1. J. Caillec, Spectral inversion of second order volterra models based on the blind identification of wiener models. Signal Process. 91(11), 2541–2555 (2011). https://doi.org/10.1016/j.sigpro.2011.05.007

    Article  MATH  Google Scholar 

  2. E. Catmull, R. Rom, A class of local interpolating splines. Comput. Aided Geom. Des. (1974). https://doi.org/10.1016/B978-0-12-079050-0.50020-5

    Article  Google Scholar 

  3. B. Chen, J.C. Principe, J. Hu, Y. Zhu, Stochastic information gradient algorithm with generalized Gaussian distribution model. J Circuits Syst. Comput. (2012). https://doi.org/10.1142/S0218126612500065

    Article  Google Scholar 

  4. B. Chen, L. Xing, H. Zhao, N. Zheng, J.C. Principe, Generalized correntropy for robust adaptive filtering. IEEE Trans. Signal Process. 64(13), 3376–3387 (2015). https://doi.org/10.1109/TSP.2016.2539127

    Article  MathSciNet  MATH  Google Scholar 

  5. D. Comminiello, M. Scarpiniti, L.A. Azpicueta-Ruiz, J. Arenas-García, A. Uncini, Functional link adaptive filters for nonlinear acoustic echo cancellation. IEEE Trans. Audio Speech Lang. Process. 21(7), 1502–1512 (2013). https://doi.org/10.1109/TASL.2013.2255276

    Article  Google Scholar 

  6. J. Gong, B. Yao, Neural network adaptive robust control of nonlinear systems in semi-strict feedback form. Automatica 37(8), 1149–1160 (2001). https://doi.org/10.1016/S0005-1098(01)00069-3

    Article  MathSciNet  MATH  Google Scholar 

  7. S. Haykin, Kalman filtering and neural networks, Wiley, (2001)

  8. L. Ji, J. Ni, Sparsity-aware normalized subband adaptive filters with jointly optimized parameters. J. Franklin Inst. 357(17), 13144–13157 (2020). https://doi.org/10.1016/j.jfranklin.2020.09.015

    Article  MathSciNet  MATH  Google Scholar 

  9. D. Jin, J. Chen, C. Richard, J. Chen, Model-driven online parameter adjustment for zero-attracting LMS. Signal Process. 152, 373–383 (2018). https://doi.org/10.1016/j.sigpro.2018.06.020

    Article  Google Scholar 

  10. X. Li, G.L. Wei, L.C. Wang, Distributed set-membership filtering for discrete-time systems subject to denial-of-service attacks and fading measurements: a zonotopic approach. Inf. Sci. 547, 49–67 (2021). https://doi.org/10.1016/j.ins.2020.07.041

    Article  MathSciNet  MATH  Google Scholar 

  11. F. Lindsten, T.B. Schon, M.I. Jordan, Bayesian semi-parametric wiener system identification. Automatica 49(7), 2053–2063 (2013). https://doi.org/10.1016/j.automatica.2013.03.021

    Article  MathSciNet  MATH  Google Scholar 

  12. C. Liu, Z. Zhang, Set-membership normalised least M-estimate spline adaptive filtering algorithm in impulsive noise. Electron. Lett. 54(6), 393–395 (2018). https://doi.org/10.1049/el.2017.4434

    Article  Google Scholar 

  13. C. Liu, Z. Zhang, X. Tang, Sign normalised spline adaptive filtering algorithms against impulsive noise. Signal Process. 148, 234–240 (2018). https://doi.org/10.1016/j.sigpro.2018.02.022

    Article  Google Scholar 

  14. Q. Liu, Y. He, Robust geman-mcclure based nonlinear spline adaptive filter against impulsive noise. IEEE Access. 8, 22571–22580 (2020). https://doi.org/10.1109/ACCESS.2020.2969219

    Article  Google Scholar 

  15. P. Lueg, Process of silencing sound oscillations, U. S. Patent 2043416 (1936)

  16. T. Ogunfunmi, Adaptive nonlinear system identification: the volterra and wiener model approaches (Springer, Berlin, Germany, 2007)

    Book  MATH  Google Scholar 

  17. V. Patel, S. Bhattacharjee, N. George, A family of logarithmic hyperbolic cosine spline nonlinear adaptive filters. Appl. Acoust. 178, 107–973 (2021). https://doi.org/10.1016/j.apacoust.2021.107973

    Article  Google Scholar 

  18. S. Peng, Z. Wu, X. Zhang, B. Chen, Nonlinear spline adaptive filtering under maximum correntropy criterion. In TENCON 2015–2015 IEEE Region 10 Conference, IEEE, pp. 1–5 (2015). https://doi.org/10.1109/TENCON.2015.7373051

  19. N. Quaegebeur, A. Chaigne, Nonlinear vibrations of loudspeaker-like structures. J. Sound Vibr. 309, 178–196 (2008). https://doi.org/10.1016/j.jsv.2007.06.040

    Article  Google Scholar 

  20. M. Rasouli, D. Westwick, W. Rosehart, Quasiconvexity analysis of the Hammerstein model. Autom. 50(1), 277–281 (2014). https://doi.org/10.1016/j.automatica.2013.11.004

    Article  MathSciNet  MATH  Google Scholar 

  21. G. Scarano, D. Caggiati, G. Jacovitti, Cumulant series expansion of hybrid nonlinear moments of n variates. IEEE Trans. Signal Process. 41(1), 486–489 (1993). https://doi.org/10.1109/TSP.1993.193184

    Article  MATH  Google Scholar 

  22. M. Scarpiniti, D. Comminiello D, R. Parisi, A. Uncini, Spline adaptive filters: theory and applications//Adaptive learning methods for nonlinear system modeling. Butterworth-Heinemann, 47–69 (2008).

  23. M. Scarpiniti, D. Comminiello, R. Parisi, A. Uncini, Nonlinear spline adaptive filtering. Signal Process. 93(4), 772–783 (2013). https://doi.org/10.1016/j.sigpro.2012.09.021

    Article  MATH  Google Scholar 

  24. M. Scarpiniti, D. Comminiello, R. Parisi, A. Uncini, Novel cascade spline architectures for the identification of nonlinear systems. IEEE Trans. Circuits Syst. I-Regul. Pap. 62(7), 1825–1835 (2015). https://doi.org/10.1109/TCSI.2015.2423791

    Article  MathSciNet  MATH  Google Scholar 

  25. M. Scarpiniti, D. Comminiello, G. Scarano, R. Parisi, A. Uncini, Steady-state performance of spline adaptive filters. IEEE Trans. Signal Process. 64(4), 816–828 (2016). https://doi.org/10.1109/TSP.2015.2493986

    Article  MathSciNet  MATH  Google Scholar 

  26. A. Singh, J. C. Principe, Using correntropy as a cost function in linear adaptive filters. In 2009 International Joint Conference on Neural Networks (IJCNN), IEEE, pp. 2950–2955 (2009). https://doi.org/10.1109/IJCNN.2009.5178823

  27. S. Talebi, S. Godsill, D. Mandic, Filtering structures for α-stable systems. IEEE Control Syst. Lett. 7, 553–558 (2023). https://doi.org/10.1109/LCSYS.2022.3202827

    Article  MathSciNet  Google Scholar 

  28. M. Varanasi, B. Aazhang, Parametric generalized gaussian density estimation. J. Acoust. Soc. Amer. 86(4), 1404–1415 (1989). https://doi.org/10.1121/1.398700

    Article  Google Scholar 

  29. X. Wang, J.H. Park, H. Liu, X. Zhang, Cooperative output-feedback secure control of distributed linear cyber-physical systems resist intermittent DoS attacks. IEEE Trans. Cybernetics. 51(10), 4924–4933 (2021). https://doi.org/10.1109/TCYB.2020.3034374

    Article  Google Scholar 

  30. P. Wen, J. Zhang, S. Zhang, B. Qu, Normalized subband spline adaptive filter: algorithm derivation and analysis. Circuits Syst. Signal Process. 40, 2400–2418 (2021). https://doi.org/10.1007/s00034-020-01577-6

    Article  Google Scholar 

  31. N. Wiener, Extrapolation, interpolation, and smoothing of stationary time series (Wiley, New York, 1964)

    Google Scholar 

  32. J. Zhang, Y. Jiang, X. Li, M. Huo, H. Luo, S. Yin, An adaptive remaining useful life prediction approach for single battery with unlabeled small sample data and parameter uncertainty. Reliab. Eng. Syst. Saf. 222, 0951–8320 (2022). https://doi.org/10.1016/j.ress.2022.108357

    Article  Google Scholar 

  33. J. Zhang, Y. Jiang, X. Li, H. Luo, S. Yin, O. Kaynak, Remaining useful life prediction of Lithium-Ion battery with adaptive noise estimation and capacity regeneration detection. IEEE/ASME Trans. Mechatron. (2022). https://doi.org/10.1109/tmech.2022.3202642

    Article  Google Scholar 

  34. J. Zhang, X. Xiao, Predicting low-dimensional chaotic time series using volterra adaptive filters. Acta Phys. Sin. 49, 403–408 (2000). https://doi.org/10.1016/S0370-2693(00)00081-2

    Article  Google Scholar 

  35. H. Zhao, Y. Gao, Y. Zhu, Robust subband adaptive filter algorithms-based mixture correntropy and application to acoustic echo cancellation. IEEE Trans. Audio Speech Lang. Process. 31, 1223–1233 (2023). https://doi.org/10.1109/TASLP.2023.3250845

    Article  Google Scholar 

  36. H. Zhao, B. Tian, Robust power system forecasting-aided state estimation with generalized maximum mixture correntropy unscented Kalman filter. IEEE Trans. Instrum. Meas. 71, 1–10 (2022). https://doi.org/10.1109/TIM.2022.3160562

    Article  Google Scholar 

  37. H. Zhao, B. Tian, B. Chen, Robust stable iterated unscented kalman filter based on maximum correntropy criterion. Automatica (2022). https://doi.org/10.1016/j.automatica.2022.110410

    Article  MATH  Google Scholar 

  38. H. Zhao, W. Xiang, S. Lv, A variable parameter LMS algorithm based on generalized maximum correntropy criterion for graph signal processing. IEEE Tran. Signal Inf. Process. Netw. 9, 140–151 (2023). https://doi.org/10.1109/TSIPN.2023.3248948

    Article  MathSciNet  Google Scholar 

  39. S. Zhou, H. Zhao, Statistics variable kernel width for maximum correntropy criterion algorithm. Signal Process. 176, 109589 (2020). https://doi.org/10.1016/j.sigpro.2020.107589

    Article  Google Scholar 

  40. Y. Zhu, H. Zhao, X. He, Z. Shu, B. Chen, Cascaded random fourier filter for robust nonlinear active noise control. IEEE Trans. Audio Speech Lang. Process. 30, 2188–2200 (2022). https://doi.org/10.1109/TASLP.2021.3126943

    Article  Google Scholar 

  41. Y. Zhu, H. Zhao, X. Zeng, B. Chen, Robust generalized maximum correntropy criterion algorithms for active noise control. IEEE Trans. Audio, Speech, Lang. Process. 28, 1282–1292, (2020). https://doi.org/10.1109/TASLP.2020.2982030

  42. Y. Zou, S. Chan, T. Ng, Least mean M-estimate algorithms for robust adaptive filtering in impulse noise. IEEE Trans. Circuits Syst. II Analog Digit. Signal Process. 47(12), 1564–1569 (2000). https://doi.org/10.1109/82.899657

Download references

Acknowledgements

This work was partially supported by National Natural Science Foundation of China (Grant Nos: 62171388, 61871461, 61571374) and Fundamental Research Funds for the Central Universities (Grant No: 2682021ZTPY091).

Author information

Authors and Affiliations

  1. Key Laboratory of Magnetic Suspension Technology and Maglev Vehicle, Ministry of Education; School of Electrical Engineering, Southwest Jiaotong University, Chengdu, 610031, China

    Yuan Gao, Haiquan Zhao, Yingying Zhu & Jingwei Lou

Authors
  1. Yuan Gao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Haiquan Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yingying Zhu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Jingwei Lou
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Haiquan Zhao.

Ethics declarations

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gao, Y., Zhao, H., Zhu, Y. et al. Spline Adaptive Filtering Algorithm-based Generalized Maximum Correntropy and its Application to Nonlinear Active Noise Control. Circuits Syst Signal Process 42, 6636–6659 (2023). https://doi.org/10.1007/s00034-023-02411-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00034-023-02411-5

Keywords

Search

Navigation