Abstract
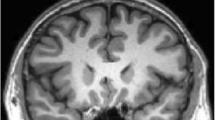
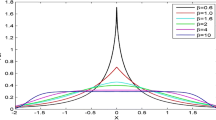
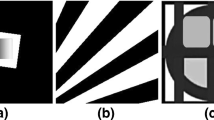
In this paper, a newfangled technique for edge detection that combines the Khalil conformable derivative and the Hessian matrix is developed and experimentally validated. The following main aspects are considered: (i) to attenuate image noise a Gaussian kernel inspired by the Khalil conformable derivative was developed. (ii) The spatial derivatives of the image gray level are calculated via the Khalil derivative, which is suitable for maintaining object contours and texture information even in low-contrast and resolution images. (iii) The conformable Hessian matrix is obtained from these image derivatives, generating continuous, thicker, and brighter edges. Our operator is compared with some existing techniques. Simulation results on different test images confirm a greater robustness to noise by our operator as well as a better visual quality of the edge maps obtained. This statement is validated through a comparative analysis based on peak signal-to-noise ratio and edge-strength-similarity-based image quality. In addition, it is applied in medical image processing and analysis tasks such as mammogram images, computed tomography scans, and magnetic resonance imaging for identification tasks of middle cerebral artery aneurysms, calcifications and breast cancer, proliferative Diabetic Retinopathy, and cerebral arteriovenous malformations. According to our findings, the conformable operator allows better visual identification of the structure of these conditions, improving the accuracy of clinical diagnosis and its subsequent monitoring.



































Similar content being viewed by others
Data Availability
No data were generated or analyzed during the current study.
References
A. Abirami, P. Prakash et al., Fractional diffusion equation for medical image denoising using adi scheme. J. Popul. Ther. Clin. Pharmacol. 30(12), 52–63 (2023). https://doi.org/10.47750/jptcp.2023.30.12.008
R.S. Aldoury, N.M. Al-Saidi, R.W. Ibrahim, H. Kahtan, A new x-ray images enhancement method using a class of fractional differential equation. MethodsX 11, 102264 (2023). https://doi.org/10.1016/j.mex.2023.102264
S. AlShamekh, Arteriovenous malformations. Dermatol. Clin. 40(4), 445–448 (2022). https://doi.org/10.1016/j.det.2022.06.012
Y. An, K. Chen, F. Nie, Echocardiography diagnosis of mitral valve aneurysm complicated with infective endocarditis. Int. Heart J. 64(5), 959–962 (2023). https://doi.org/10.1536/ihj.23-121
J.K. Appati, E. Owusu, M. Agbo Tettey Soli, K.S. Adu-Manu, A novel convolutional Atangana–Baleanu fractional derivative mask for medical image edge analysis. J. Exp. Theor. Artif. Intell. (2022). https://doi.org/10.1080/0952813X.2022.2108147
A. Asokan, J. Anitha, Edge preserved satellite image denoising using median and bilateral filtering, in Recent Trends in Image Processing and Pattern Recognition. ed. by K.C. Santosh, R.S. Hegadi (Springer, Singapore, 2019), pp.688–699. https://doi.org/10.1007/978-981-13-9181-1_59
V. Babu, Basilar top and left middle cerebral artery aneurysm. Case study, Radiopaedia.org (2018). Accessed 22 Feb 2024. https://doi.org/10.53347/rID-61965
S. Balochian, H. Baloochian, Edge detection on noisy images using Prewitt operator and fractional order differentiation. Multimedia Tools Appl. 81(7), 9759–9770 (2022). https://doi.org/10.1007/s11042-022-12011-1
A. Ben-loghfyry, A. Hakim, A novel robust fractional-time anisotropic diffusion for multi-frame image super-resolution. Adv. Comput. Math. 49(6), 79 (2023). https://doi.org/10.1007/s10444-023-10079-3
K. Benyettou, D. Bouagada, On the positivity of fractional two-dimensional systems using the non-conformable derivative. Int. J. Dyn. Control 11(6), 2751–2762 (2023). https://doi.org/10.1007/s40435-023-01137-1
W. Burger, M.J. Burge, Digital Image Processing: An Algorithmic Introduction (Springer, London, 2022). https://doi.org/10.1007/978-1-4471-6684-9
J.F. Cavalcante-Neto, G.d.A. Monteiro, A.B. Brandt, G.E.P. Soares, D.J.F. Solla, P.R.L. Leal, G. Cristino-Filho, K.F. da Ponte, Rete middle cerebral artery aneurysm: a case report and systematic review. Asian J. Neurosurg. 18(04), 790–795 (2023). https://doi.org/10.1055/s-0043-1775732
F. Çetinkaya, A review on the evolution of the conformable derivative. Funct. Differ. Equ. 29, 1–2 (2022). https://doi.org/10.26351/FDE/29/1-2/2
L. Chen, J. Gao, A.M. Lopes, Z. Zhang, Z. Chu, R. Wu, Adaptive fractional-order genetic-particle swarm optimization Otsu algorithm for image segmentation. Appl. Intell. 53(22), 26949–26966 (2023). https://doi.org/10.1007/s10489-023-04969-8
Y. Chen, Y. Yao, H. Yang, Y. Wu, K. Zhang, X. Pan, Curvature-based machine vision method for measuring the dimension of ball screws. IEEE Access 11, 126803–126813 (2023). https://doi.org/10.1109/ACCESS.2023.3328555
D. Cuete, Cerebral arteriovenous malformation. Case study, Radiopaedia.org (2016). Accessed 22 Feb 2024. https://doi.org/10.53347/rID-43729
D. Cuete, Middle cerebral artery aneurysm. Case study, Radiopaedia.org (2014). Accessed 22 Feb 2024. https://doi.org/10.53347/rID-29423
F. Gaillard, Arteriovenous malformation - cerebral. Case study, Radiopaedia.org (2010). Accessed 22 Feb 2024. https://doi.org/10.53347/rID-8172
F. Gaillard, Hemorrhagic hereditary telangiectasia. Case study, Radiopaedia.org (2016). Accessed 22 Feb 2024. https://doi.org/10.53347/rID-29967
F. Gaillard, Spiculated breast cancer. Case study, Radiopaedia.org (2010). Accessed 22 Feb 2024. https://doi.org/10.53347/rID-12608
S. Gamini, V.V. Gudla, C.H. Bindu, Fractional-order diffusion based image denoising model. Int. J. Electr. Electron. Res. (IJEER) 10(4), 837–842 (2022). https://doi.org/10.37391/ijeer.100413
N.M. Hassan, S. Hamad, K. Mahar, Mammogram breast cancer cad systems for mass detection and classification: a review. Multimed. Tools Appl. 81(14), 20043–20075 (2022). https://doi.org/10.1007/s11042-022-12332-1
F.I. Himasa, M. Singhal, A. Ojha, B. Kumar, Prospective for diagnosis and treatment of diabetic retinopathy. Curr. Pharm. Des. 28(7), 560–569 (2022). https://doi.org/10.2174/1381612827666211115154907
A. Hoover, M. Goldbaum, Locating the optic nerve in a retinal image using the fuzzy convergence of the blood vessels. IEEE Trans. Med. Imaging 22(8), 951–958 (2003). https://doi.org/10.1109/TMI.2003.815900
T. Huang, X. Wang, C. Wang, X. Liu, Y. Yu, W. Qiu, Super-resolution reconstruction algorithm for depth image based on fractional calculus. In: 35th Chinese Control and Decision Conference (CCDC), pp. 389–396. IEEE (2023). https://doi.org/10.1109/CCDC58219.2023.10326972
T. Huang, X. Wang, D. Xie, C. Wang, X. Liu, Depth image enhancement algorithm based on fractional differentiation. Fractal Fract. 7(5), 394 (2023). https://doi.org/10.3390/fractalfract7050394
D. Ibrahim, Cerebral arteriovenous malformation. Case study, Radiopaedia.org (2014). Accessed 22 Feb 2024. https://doi.org/10.53347/rID-29531
R.W. Ibrahim, H.A. Jalab, F.K. Karim, E. Alabdulkreem, M.N. Ayub, A medical image enhancement based on generalized class of fractional partial differential equations. Quant. Imaging Med. Surg. 12(1), 172 (2022). https://doi.org/10.21037/qims-21-15
B. Jähne, H. Haussecker, P. Geissler, Handbook of Computer Vision and Applications, vol. 2 (Citeseer, USA, 1999)
M. Joshi, S. Bhosale, V.A. Vyawahare, A survey of fractional calculus applications in artificial neural networks. Artif. Intell. Rev. 56(11), 13897–13950 (2023). https://doi.org/10.1007/s10462-023-10474-8
F.K. Karim, H.A. Jalab, R.W. Ibrahim, R. Ala’a, Mathematical model based on fractional trace operator for COVID-19 image enhancement. J. King Saud Univer.-Sci. 34(7), 102254 (2022). https://doi.org/10.1016/j.jksus.2022.102254
R. Khalil, M. Al Horani, A. Yousef, M. Sababheh, A new definition of fractional derivative. J. Comput. Appl. Math. 264, 65–70 (2014). https://doi.org/10.1016/j.cam.2014.01.002
M.A. Khan, A. Ullah, Z.-J. Fu, S. Khan, S. Khan, Image restoration via combining a fractional order variational filter and a TGV penalty. Multimedia Tools Appl. (2024). https://doi.org/10.1007/s11042-023-17774-9
M. Khan, P. Kumar, A nonlinear modeling of fractional order based variational model in optical flow estimation. Optik 261, 169136 (2022). https://doi.org/10.1016/j.ijleo.2022.169136
M. Khan, N.K. Mahala, P. Kumar, Caputo derivative based nonlinear fractional order variational model for motion estimation in various application oriented spectrum. Sādhanā 49(1), 1–28 (2024). https://doi.org/10.1007/s12046-023-02318-6
G. Kruger, Ductal carcinoma in situ in an invasive ductal carcinoma. Case study, Radiopaedia.org (2012). Accessed 22 Feb 2024. https://doi.org/10.53347/rID-19035
G. Kruger, Fat necrosis - breast. Case study, Radiopaedia.org (2013). Accessed 22 Feb 2024. https://doi.org/10.53347/rID-21553
G. Kruger, Invasive ductal carcinoma. Case study, Radiopaedia.org (2013). Accessed 22 Feb 2024. https://doi.org/10.53347/rID-23260
G. Kruger, Liponecrotic breast calcifications. Case study, Radiopaedia.org (2013). Accessed 22 Feb 2024. https://doi.org/10.53347/rID-21895
P. Kumar, M. Khan, N.K. Mahala, A segmentation based robust fractional variational model for motion estimation. In: International Conference on Computer Vision and Image Processing, vol. 1776, pp. 115–128. Springer (2022). https://doi.org/10.1007/978-3-031-31407-0_9
S. Kumar, M.K. Gupta, A.S. Shekhawat, Fractional calculus and special functions with applications in applied mathematics and other sciences—a review. Int. J. Converg. Technol. Manag. 9(1), 74–82 (2023)
J. Lavín-Delgado, J. Gómez-Aguilar, D. Urueta-Hinojosa, Z. Zamudio-Beltrán, J. Alanís-Navarro, An efficient technique for object recognition using fractional Harris–Stephens corner detection algorithm. Multimed. Tools Appl. 83(8), 23173–23199 (2023). https://doi.org/10.1007/s11042-023-16428-0
M. Madaminov, F. Shernazarov, Breast cancer detection methods, symptoms, causes, treatment. Sci. innov. 1(D8), 530–535 (2022). https://doi.org/10.5281/zenodo.7401437
A. Makandar, S. Kaman, R. Biradar, S.B. Javeriya, Impact of edge detection algorithms on different types of images using PSNR and MSE. LC Int. J. STEM 3(4), 1–11 (2022). https://doi.org/10.5281/zenodo.7607059
M. Mansouri, E. Therasse, E. Montagnon, Y.O. Zhan, S. Lessard, A. Roy, L.-M. Boucher, O. Steinmetz, E. Aslan, A. Tang, et al., Ct analysis of aortic calcifications to predict abdominal aortic aneurysm rupture. Eu. Radiol. (2023). https://doi.org/10.1007/s00330-023-10429-1
D. Martin, C. Fowlkes, D. Tal, J. Malik, et al., A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics. In: Proceedings 8th IEEE International Conference on Computer Vision, vol. 2, pp. 416–423. IEEE (2001). https://doi.org/10.1109/ICCV.2001.937655
C.J. Miosso, A. Bauchspiess, Fuzzy inference system applied to edge detection in digital images. In: Proceedings of the V Brazilian Conference on Neural Networks, pp. 481–486 (2016). https://doi.org/10.21528/CBRN2001-102
M. Mortazavi, M. Gachpazan, M. Amintoosi, Improving canny edge detection algorithm using fractional-order derivatives. J. Math. Model. 10(4), 495–514 (2022). https://doi.org/10.22124/JMM.2022.21875.1921
M.A.S. Murad, Modified integral equation combined with the decomposition method for time fractional differential equations with variable coefficients. Appl. Math.—A J. Chin. Univer. 37(3), 404–414 (2022). https://doi.org/10.1007/s11766-022-4159-5
D. Nicoletti, Middle cerebral artery aneurysm. Case study, Radiopaedia.org (2016). Accessed 22 Feb 2024. https://doi.org/10.53347/rID-43168
C. O’Sullivan, S. Coveney, X. Monteys, S. Dev, The effectiveness of edge detection evaluation metrics for automated coastline detection. In: 2023 Photonics and Electromagnetics Research Symposium (PIERS), pp. 31–40. IEEE (2023). https://doi.org/10.1109/PIERS59004.2023.10221292
R. Parvaz, Image restoration with impulse noise based on fractional-order total variation and framelet transform. SIViP 17(5), 2455–2463 (2023). https://doi.org/10.1007/s11760-022-02462-2
R.J. Rahme, R. Singh, N. De La Pena, E.L. Turcotte, B.R. Bendok, Arteriovenous malformations: Treatment and management, in Introduction to Vascular Neurosurgery. ed. by J.R. Mascitelli, M.J. Binning (Springer, Switzerland, 2022), pp.389–410. https://doi.org/10.1007/978-3-030-88196-2_20
K.V. Rani, M.E. Prince, P.S. Therese, P.J. Shermila, E.A. Devi, Content-based medical image retrieval using fractional Hartley transform with hybrid features. Multimedia Tools Appl. 83(9), 27217–27242 (2023). https://doi.org/10.1007/s11042-023-16462-y
Y. Saijo, T. Orihara, N. Kanno, H. Yagami, T. Ishii, Estimation of fractional flow reserve in coronary artery based on serial intravascular ultrasound images. In: 2023 IEEE International Ultrasonics Symposium (IUS), pp. 1–3. IEEE (2023). https://doi.org/10.1109/IUS51837.2023.10307832
R. Sharma, B. Goyal, A. Dogra, Advancement in diabetic retinopathy diagnosis techniques: automation and assistive tools. Open Neuroimaging J. 16(1), 1–10 (2023). https://doi.org/10.2174/18744400-v16-230831-2022-1
H. Singh, H. Srivastava, R. Pandey, Special Functions in Fractional Calculus and Engineering, 1st edn. (CRC Press, Boca Raton, 2023)
R. Sun, T. Lei, Q. Chen, Z. Wang, X. Du, W. Zhao, A.K. Nandi, Survey of image edge detection. Front. Signal Process. 2, 826967 (2022). https://doi.org/10.3389/frsip.2022.826967
K.G. Vishnu, K.E. Bhageerath, A.V. Pallanti, A comparative analysis of edge detection techniques for processing of a video signal. Int. J. Adv. Netw. Appl. 13(4), 5029–5036 (2022)
Y. Wang, F. Xiong, J. Leach, E. Kao, B. Tian, C. Zhu, Y. Zhang, M. Hope, D. Saloner, D. Mitsouras, Contrast-enhanced CT radiomics improves the prediction of abdominal aortic aneurysm progression. Eur. Radiol. 33(5), 3444–3454 (2023). https://doi.org/10.1007/s00330-023-09490-7
X.-J. Wu, Q. Zhao, M.-Y. Gao, S.-K. Xu, S.-X. Liu, Image reconstruction algorithm of electromagnetic tomography based on fractional Kalman filter. Flow Meas. Instrum. 86, 102198 (2022). https://doi.org/10.1016/j.flowmeasinst.2022.102198
Y. Yang, H.H. Zhang, Fractional Calculus with Its Applications in Engineering and Technology, 1st edn. (Springer, Switzerland, 2022)
D. Zhang, Y. Lin, H. Chen, Z. Tian, X. Yang, J. Tang, K.T. Cheng, Deep learning for medical image segmentation: tricks, challenges and future directions. arXiv preprint arXiv:2209.10307 (2022)
X. Zhang, X. Feng, W. Wang, W. Xue, Edge strength similarity for image quality assessment. IEEE Signal Process. Lett. 20(4), 319–322 (2013). https://doi.org/10.1109/LSP.2013.2244081
Acknowledgements
J.E. Lavín-Delgado, J.E. Solís-Pérez, J.F. Gómez-Aguilar and José R. Razo-Hernández acknowledges the support provided by SNI-CONAHCyT. The fifth and sixth authors would like to thank Azarbaijan Shahid Madani University. Also, the authors would like to thank dear reviewers for their constructive comments to improve the quality of the paper.
Funding
No funds were received for this paper.
Author information
Authors and Affiliations
Contributions
The authors declare that the study was realized in collaboration with equal responsibility. All authors read and approved the final manuscript.
Corresponding authors
Ethics declarations
Conflict of interest
The authors declare that they have no Conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Lavín-Delgado, J.E., Solís-Pérez, J.E., Gómez-Aguilar, J.F. et al. An Improved Object Detection Algorithm Based on the Hessian Matrix and Conformable Derivative. Circuits Syst Signal Process 43, 4991–5047 (2024). https://doi.org/10.1007/s00034-024-02669-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00034-024-02669-3